Loading... ## 0-1 分布 0-1 分布的条件: - 只进行一次事件试验 - 该试验只有两个结果 - 两个结果互不相容 $$ P(X=k)=p^k(1-p)^{1-k} $$ 其中$k=0,1;0<p<1$ 数学期望$E(X)=p$;方差$D(X)=p(1-p)$ 0-1 分布最显著的特征就是$E(X)=p$ ## 二项分布 二项分布的条件: - 每次试验都有两种不同的结果 - 两种结果是互不相容的 - 任一结果在每次试验中都有恒定的概率 - 试验间应是独立的(放回抽样) ### 二项分布的概率函数 $$ p(x) = C_{n}^x \varphi^x (1-\varphi)^{n-x} $$ 此式正是二项展开式的第$x+1$项 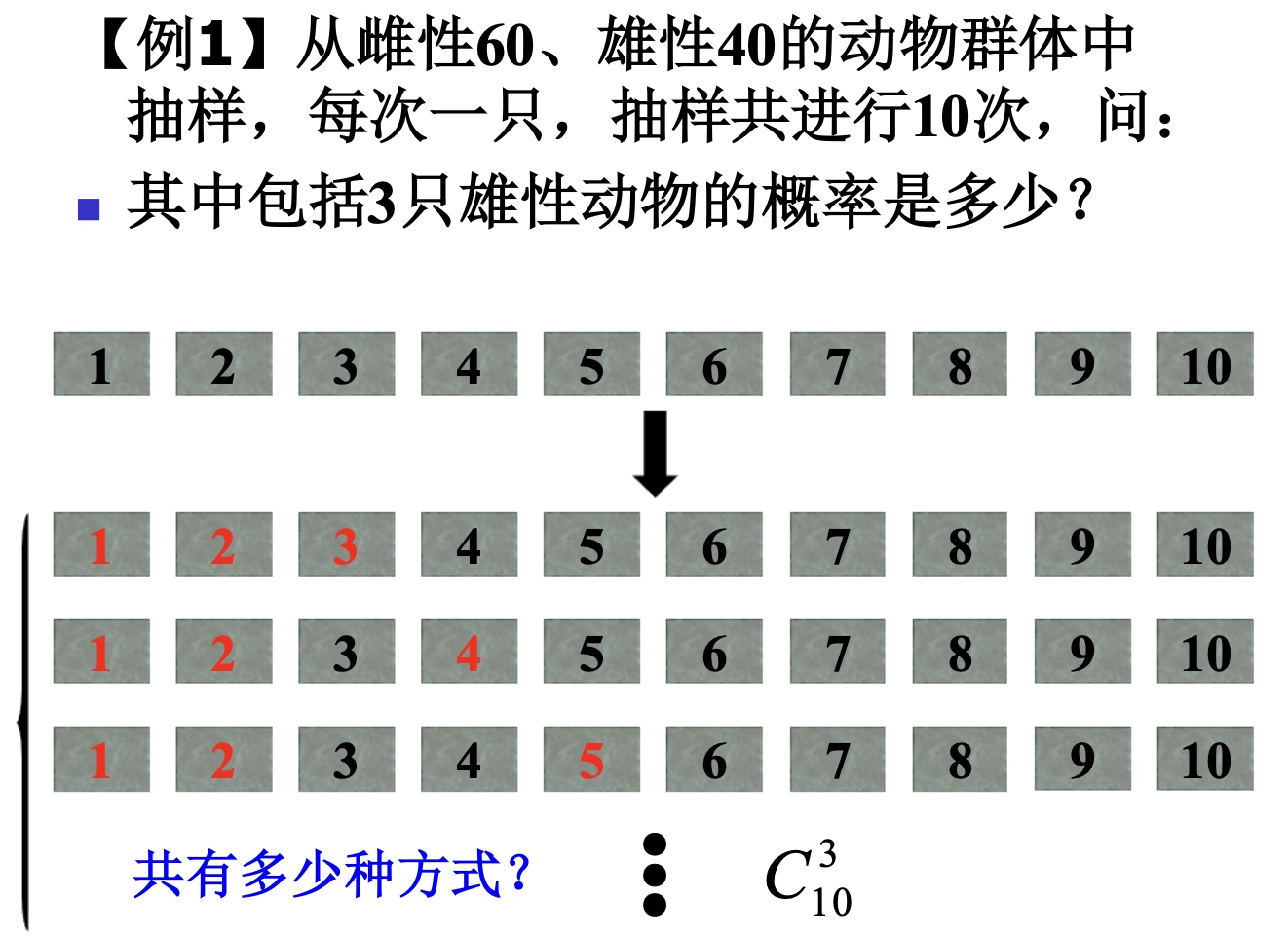   ### 二项分布的特征数 如果一个概率分布满足二项分布,则: - 平均数:$\mu=n\varphi$或$\mu=\varphi$ - 方差:$\sigma^2=n\varphi(1-\varphi)$或$\sigma^2={{\varphi(1-\varphi)}\over{n}}$ 目前可以通过比较平均值和方差来判断是否满足二项分布  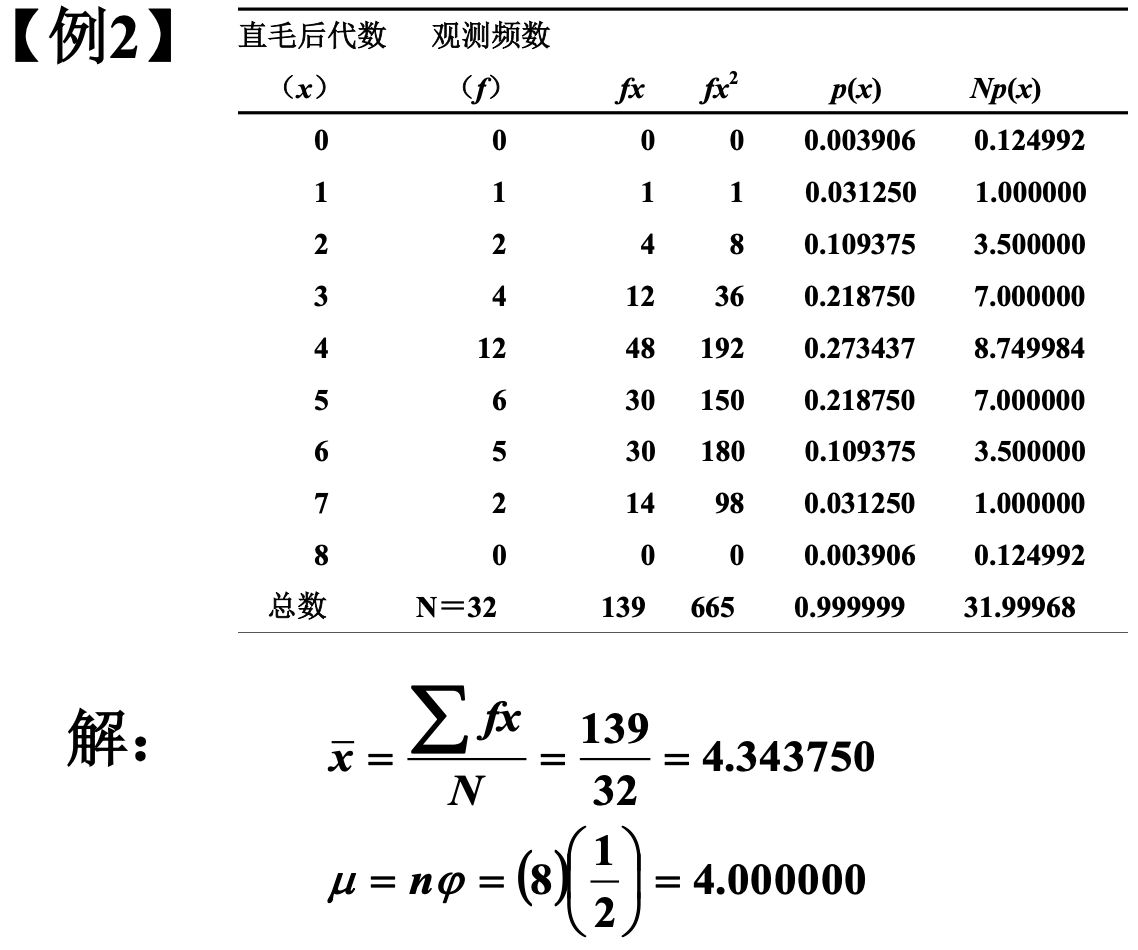 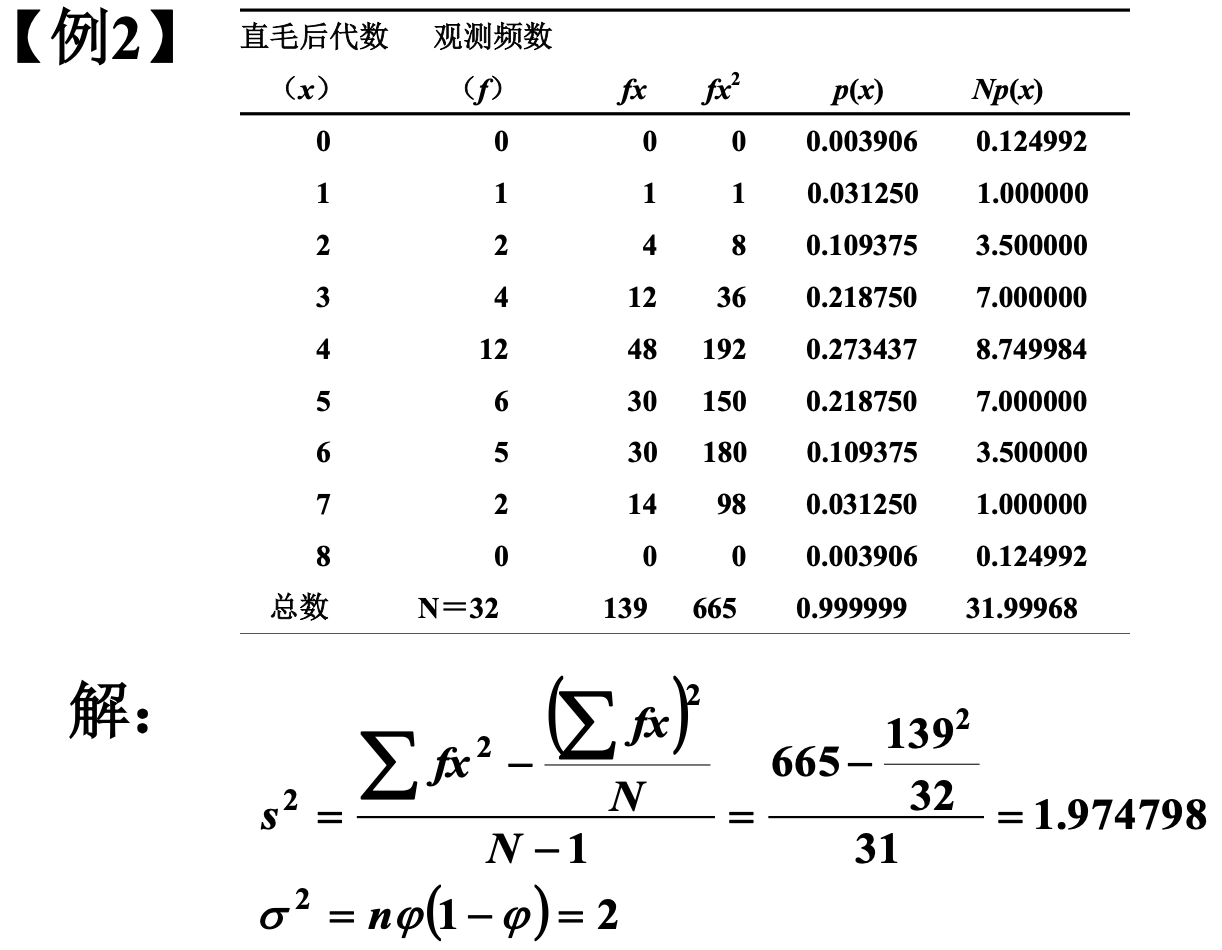 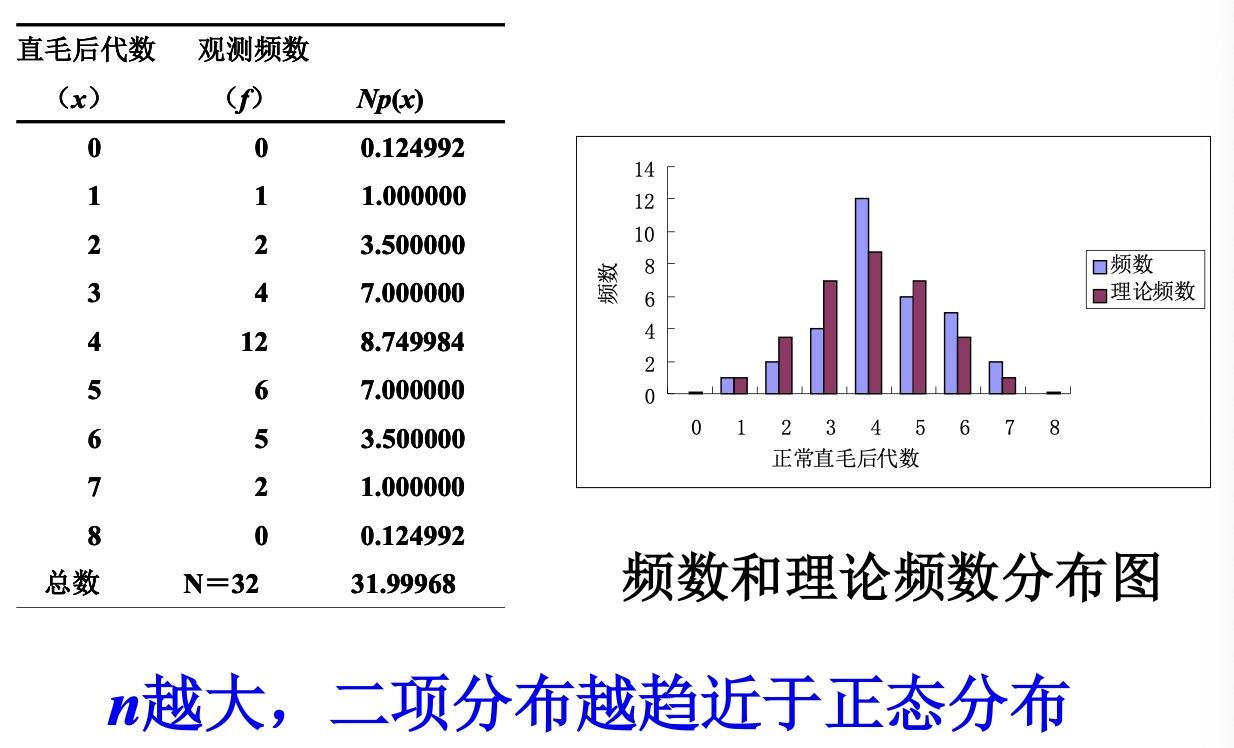 ## 泊松分布 柏松分布是二项分布的近似: - 某事件出现的概率特别小($\varphi \to 0$) - 样本含量大($n \to \infty$) $$ C_{n}^x \phi^x(1-\phi)^{n-x} \approx {\mu^x \over{x!}}(x=0,1,2,\dots \mu=n \phi) $$ ### 柏松分布的特征数 - 柏松分布的平均数:$\mu=\mu$ - 柏松分布的方差:$\sigma^2=\mu$ ### 柏松分布的特征  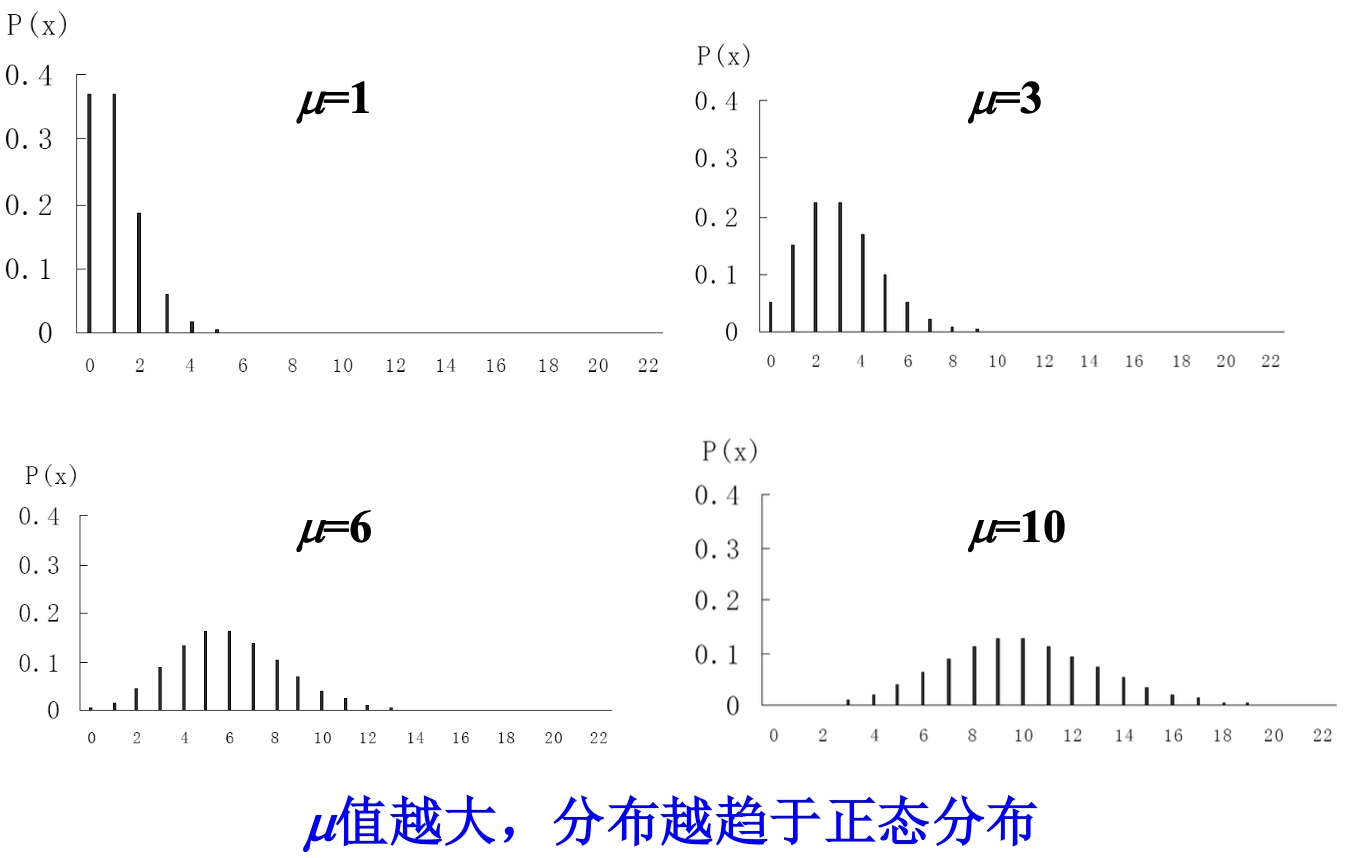 ### 柏松分布的检验   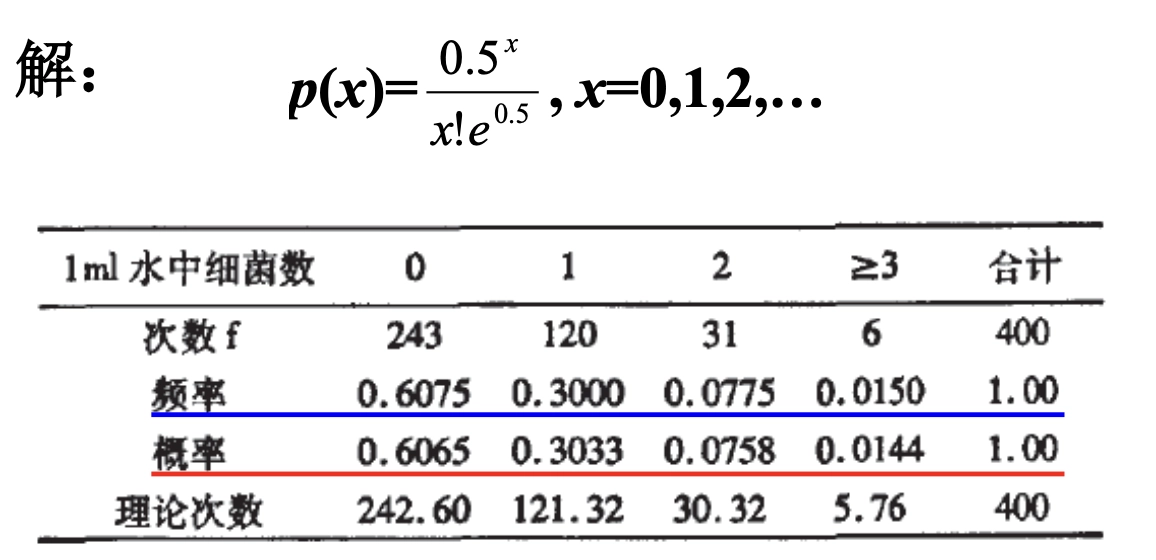 ## 正态分布 正态分布是生物统计学的重要基础 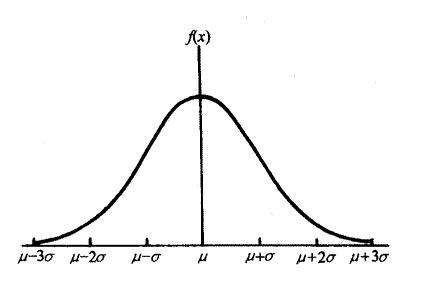 ### 正态分布的密度函数 若随机变量$X$服从一个数学期望为$\mu$、标准差为$\sigma$的高斯分布,可以记为$X\sim N(\mu, {\sigma}^2)$,其密度函数为: $$ f(x)={1\over{\sigma \sqrt{ 2\pi }}}e^{-{{(x-\mu)^2}\over{2\sigma^{2}}}}, -\infty<x<\infty,\sigma>0 $$ ### 正态概率密度函数的几何特征 - 曲线关于$x=\mu$ - 当$x=\mu$,取得最大值 - 当$x \to \pm \infty$,$p(x) \to 0$ - 曲线在$x=\mu \pm \sigma$有拐点 - 曲线以$x$轴为渐近线 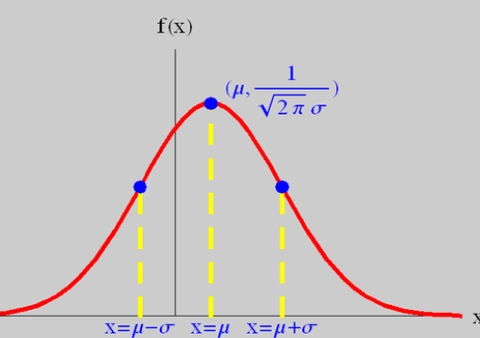 ### 正态概率密度函数的几何特征 #### 固定 $\sigma$,改变$\mu$的大小 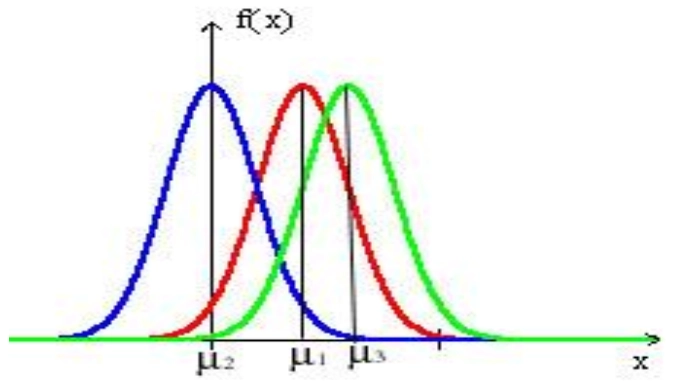 此时$f(x)$图像不变,仅沿着$x$轴作平移变换(右加左减) #### 固定$\mu$,改变$\sigma$的大小 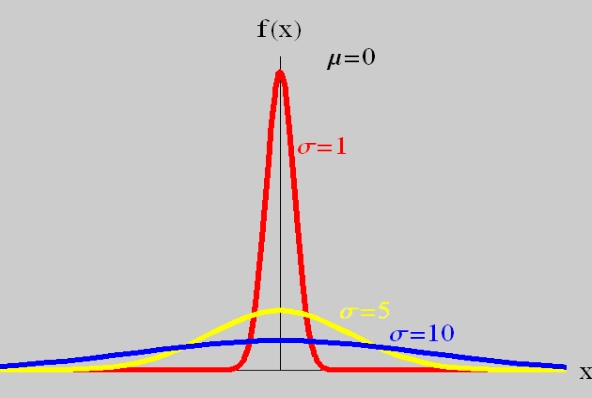 $f(x)$图像的对称轴不变,而形状改变($\sigma$越大图像越扁) #### 理解 要根据实际的统计意义来理解,其中$\mu$指的是平均数,$\sigma$则是标准差 全体样本是均匀散布在平均数左右两侧的,故$\mu$作为对称轴;$\sigma$作为标准差,反映数据的离散程度,故数据越集中,图像将越尖,反之则越扁 ### 3$\sigma$原理 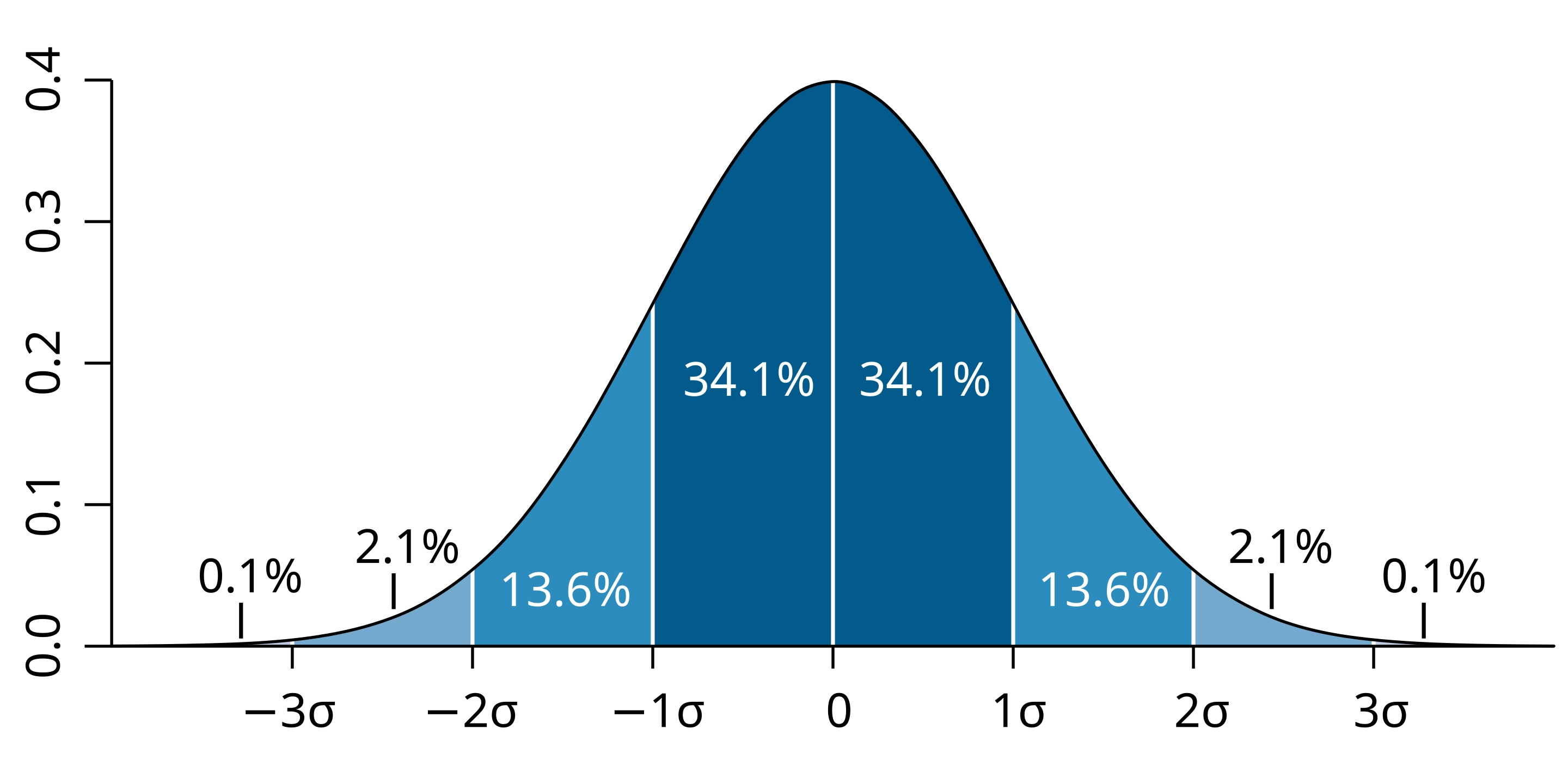 深蓝色区域是距平均值小于一个标准差之内的数值范围。在正态分布中,此范围所占比率为全部数值之68%,根据正态分布,两个标准差之内的比率合起来为95%;三个标准差之内的比率合起来为99% ### 标准正态分布 当$\mu=0$,$\sigma=1$时当正态分布被称为标准正态分布,标准正态分布记为$N(0,1)$ 标准正态分布的密度函数: $$ \varphi(u) = \frac{1}{\sqrt{2\pi}} e^{-\frac{u^2}{2}}, \quad -\infty < u < \infty $$ 累积分布函数为: $$ \Phi(u) = P(U < u) = \frac{1}{\sqrt{2\pi}} \int_{-\infty}^{u} e^{-\frac{v^2}{2}} \, dv $$ 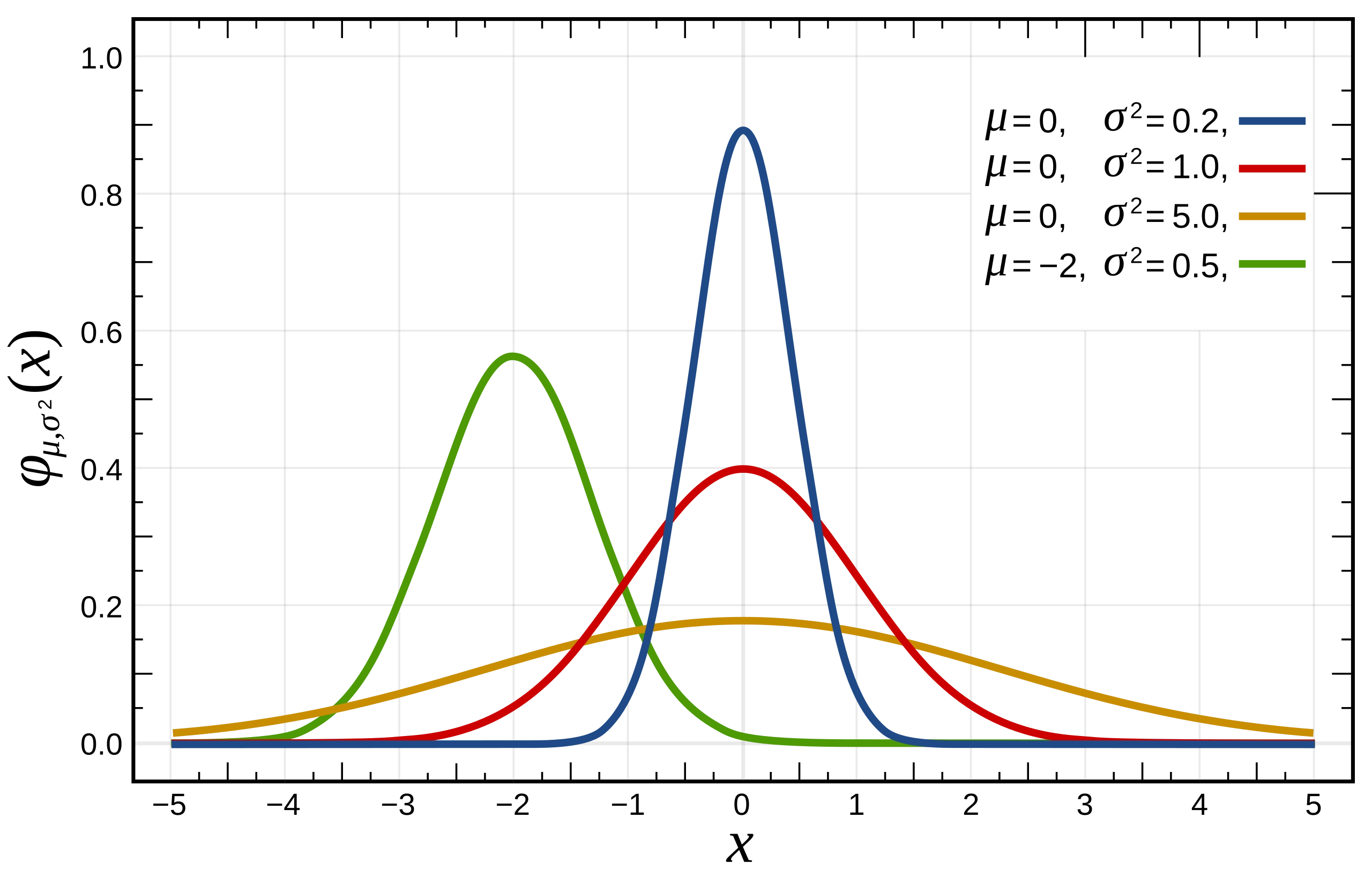 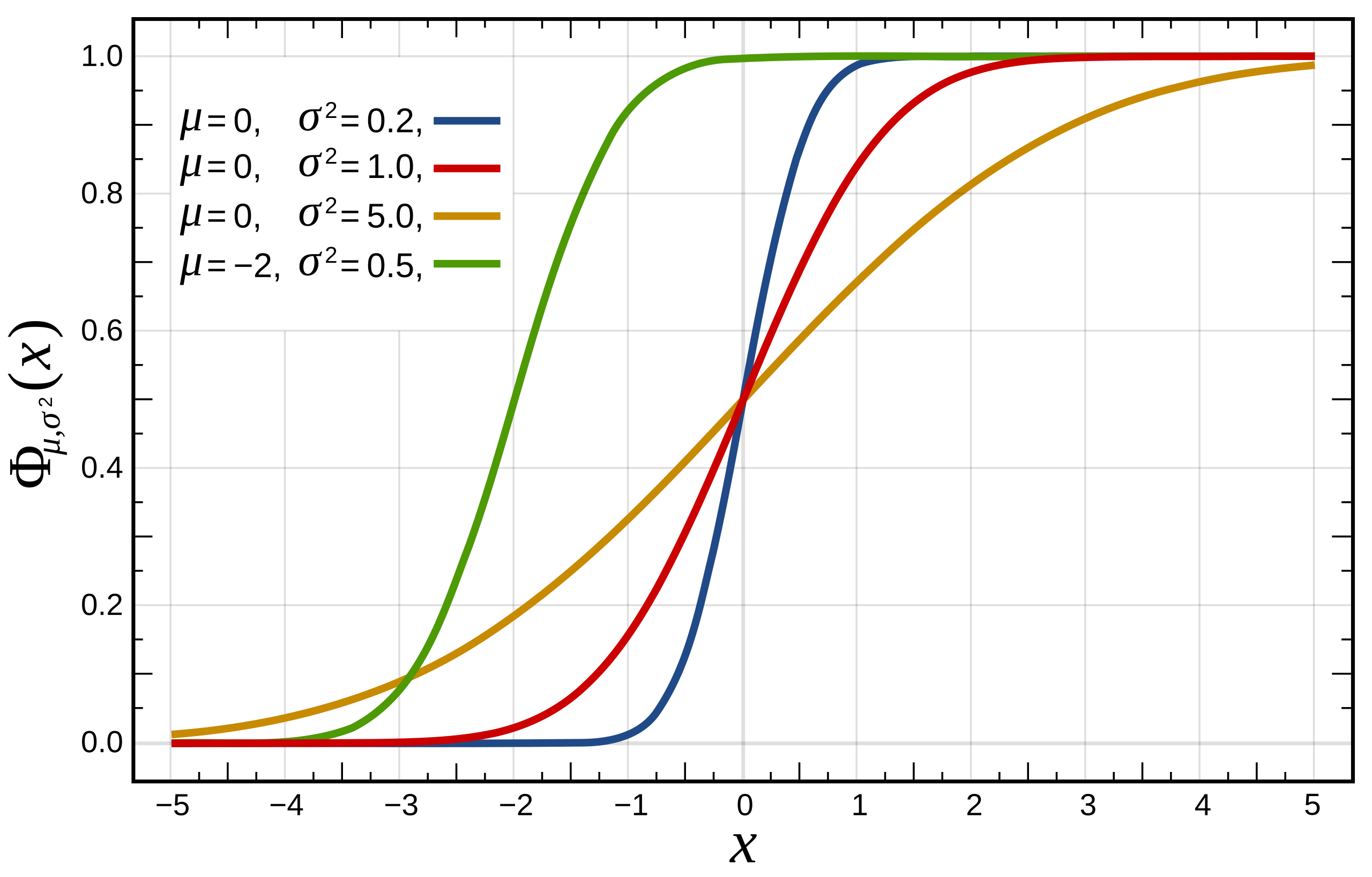 累积分布函数是密度函数的积分,如果想要查密度函数下面的面积,则可去查累积分布函数上对应的$y$坐标 ### 标准正态转化公式 标准正态转化公式用于将任意服从均值$\mu$和方差$\sigma^2$的正态分布$X\sim N(\mu,\sigma^2)$转化成标准正态分布$Z\sim N(0,1)$: $$ Z = {{X-\mu}\over{\sigma}} $$ 其中: - $X$是原始正态分布变量,$X\sim N(\mu,\sigma^2)$ - $\mu$为均值 - $\sigma$为标准差($\sigma = \sqrt{ \sigma^2 }$ ) - $Z$是转换后的标准正态分布,服从标准正态分布$N(0,1)$ 转换后就可以从标准正态分布的表中查找对应的概率  ### 正态分布的单侧分位数 正态分布的单侧分位数指的是在正态分布中,从一侧(通常是左侧或右侧)累积概率达到某个预设水平时所对应的数值。简单来说,就是你希望知道有多少比例的数据落在这个数值的某一边。例如: - **左侧分位数:** 如果你取 5% 左侧分位数,则表示在正态分布中,有 5% 的数据值落在这个数值或以下,即 P(X ≤ x) = 0.05。 - **右侧分位数:** 同样地,如果取 95% 右侧分位数,也就是有 95% 的数据值落在该数值或以下,但通常这种情况我们还是会转换为左侧描述,例如 P(X ≤ x) = 0.95。 这种概念在统计推断和假设检验中尤为重要,尤其是当你进行单侧检验时(例如,只关注比某个阈值更高或更低的情况)。计算时,通常会使用正态分布的累积分布函数(CDF)的反函数来确定对应的分位数。 选择特定的概率(比如5%或95%)确实是人为设定的标准,也就是说你确定了要关注哪一侧的那一小部分概率;但一旦确定了这个概率,所对应的分位数数值就是由正态分布的数学性质严格计算出来的,并不是任意选取的。因此,分位数既包含了人为选择的成分,也有严格的数学定义 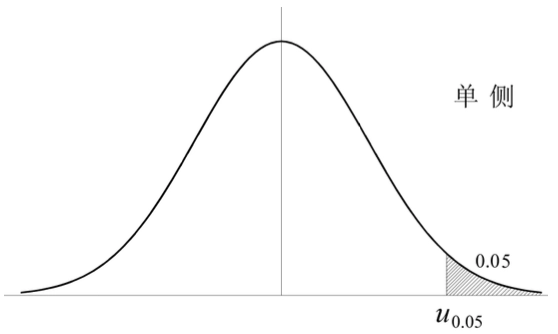 ## 指数分布 ### 指数分布密度函数 $$ p(x) = \begin{cases} \lambda e^{-\lambda x}, & x > 0 \\ 0, & x \leq 0 \end{cases} $$ 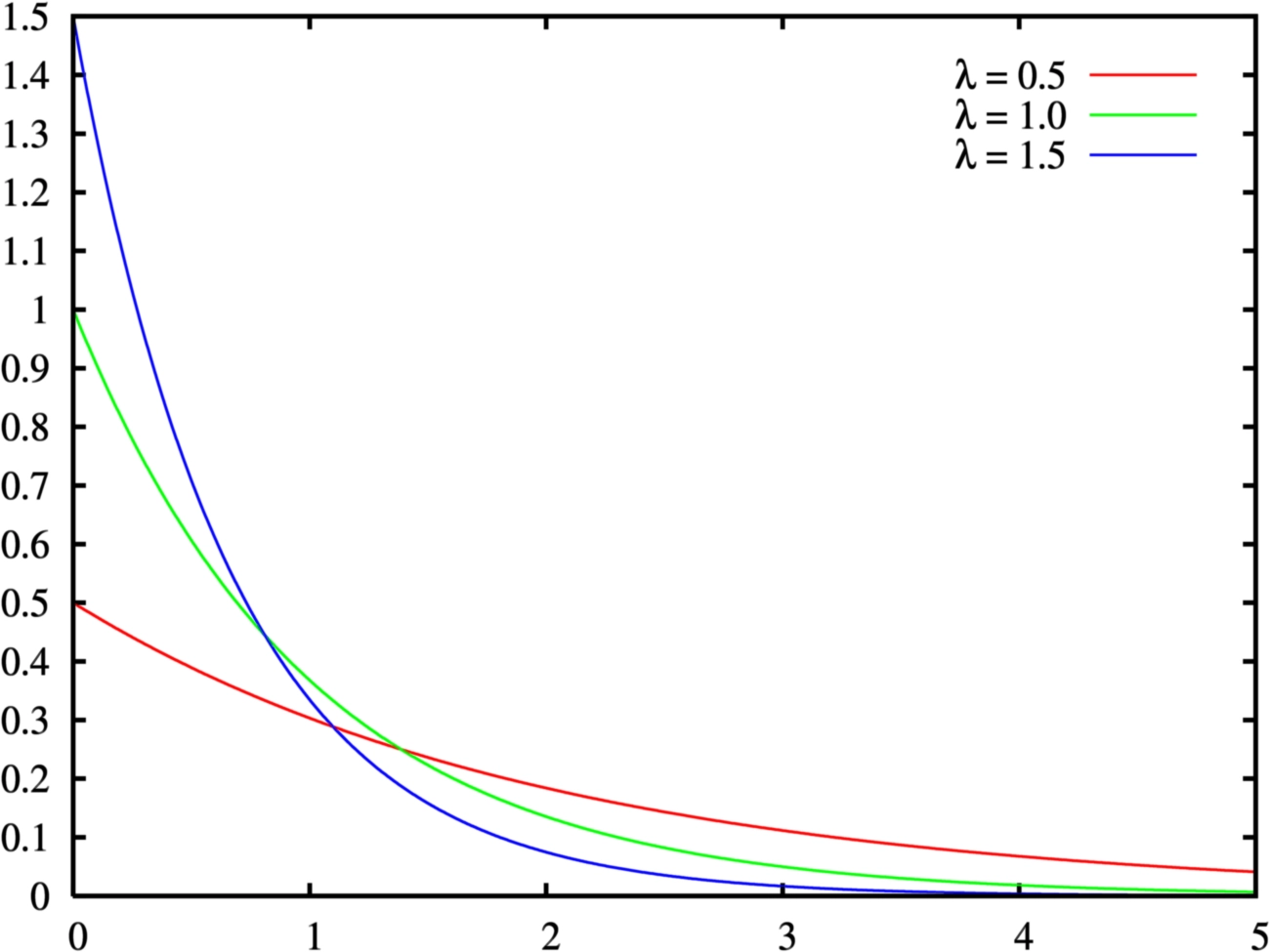 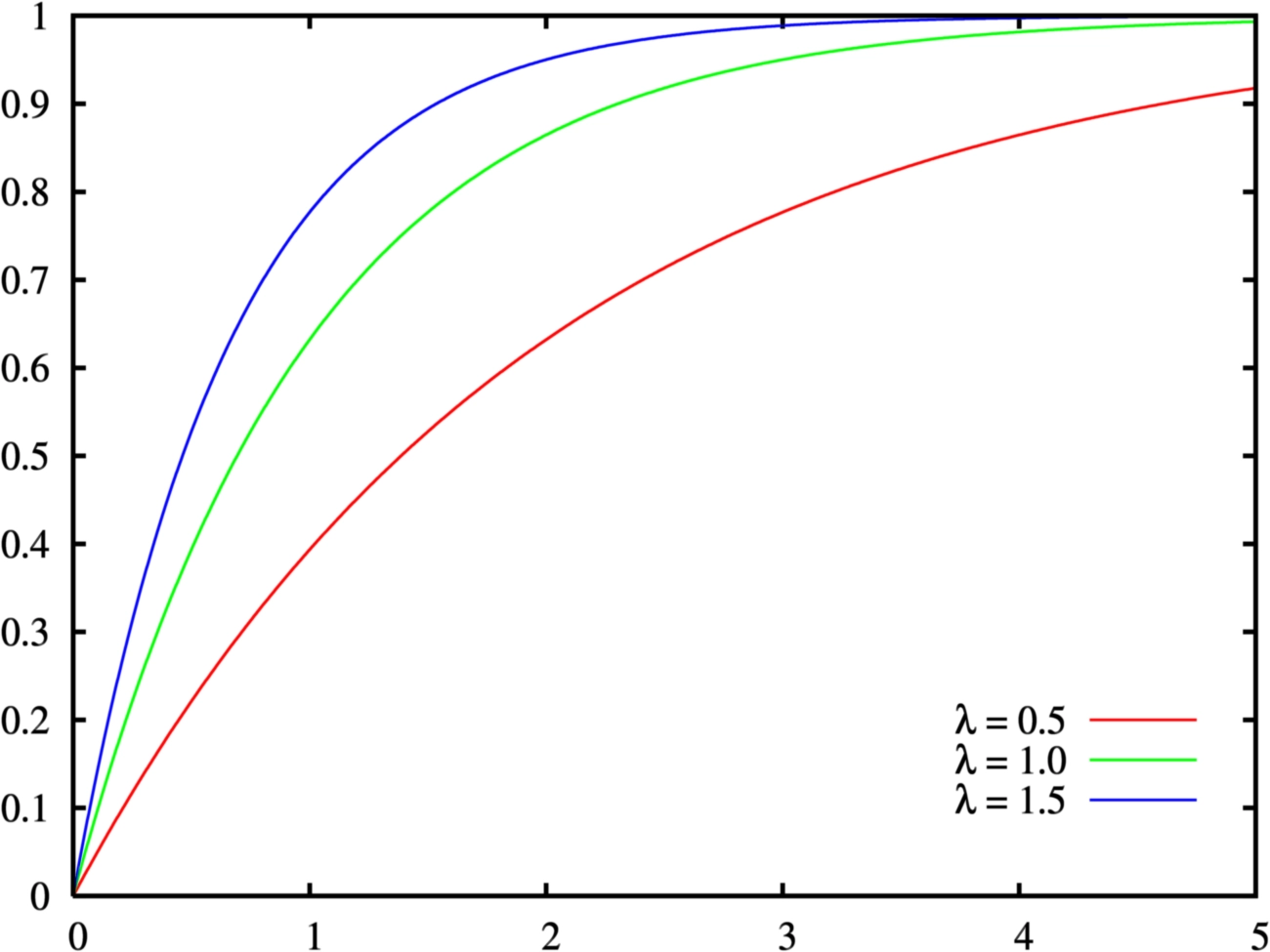 ### 指数分布的应用 指数分布可以用来表示独立时间的发生的时间间隔,生物学中经常使用指数分布描述生物的生长过程  ## 中心极限定理 中心极限定理是统计学中的一个非常重要的定理,它告诉我们:**无论原始数据的分布是什么,只要我们把大量独立的随机变量(例如测量值、抽样数据等)相加或取平均,最终的结果会接近正态分布** ### 中心极限定理的条件 $$ X=X_{1}+X_{2}+\dots+X_{n}=\sum_{i=1}^nX_{i} $$ $$ \mu_{X}=\mu_{1}+\mu_{2}+\dots+\mu_{n}=\sum_{i=1}^n\mu_{i} $$ $$ \sigma_{X}^2=\sigma_{1}^2+\sigma_{2}^2+\dots+\sigma_{n}^2=\sum_{i=1}^n\sigma_{i}^2 $$ ### 数学表述 设$X_{1},X_{2},\dots,X_{n}$是一组相互独立且分布相同的随机变量,每个变量的期望为$\mu$(有限)和方差为$\sigma^2$(有限),令样本均值为: $$ \bar{X_{n}}={\frac{1}{n}}\sum_{i=1}^nX_{i} $$ 中心极限定理表明,当$n$足够大时,标准化后的样本均值: $$ Z_{n}={{\bar{X}-\mu}\over{\sigma/\sqrt{n}}} $$ 近似服从标准正态分布$N(0,1)$ 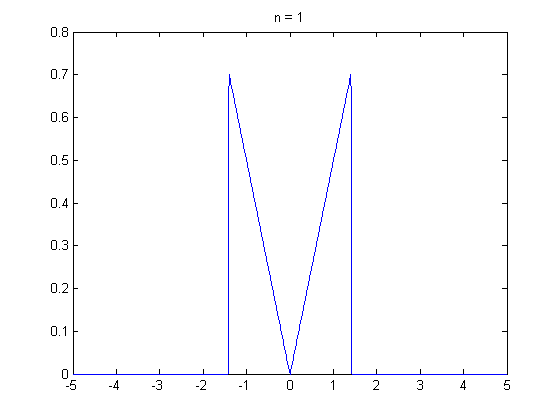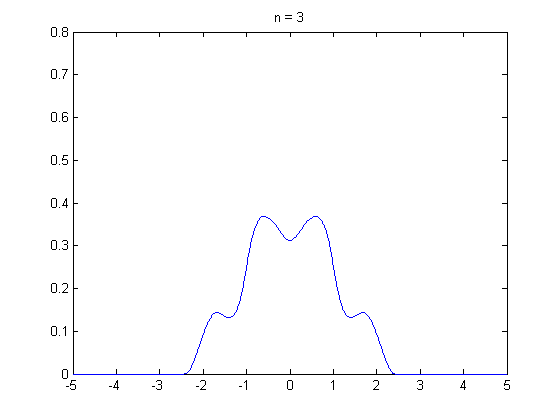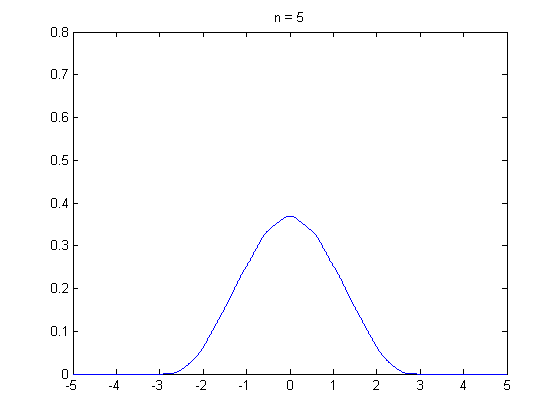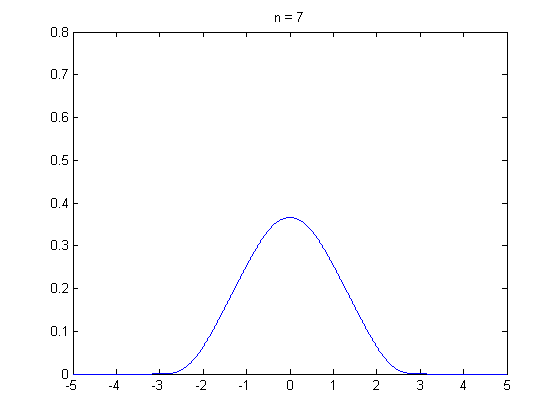 最后修改:2025 年 03 月 22 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏
此处评论已关闭