Loading... ## 数据类型 ### 离散型随机变量 - **离散型数据**:由记录不同类别个体的数目所得到的数据,又称为计数数据 - **离散型随机变量**:其数值只能用自然数或整数单位表示,例如,企业个数,职工人数,设备台数等 **例如**:某地某日新生儿的出生人数 ### 连续性随机变量 - **连续型数据**:与某种标准做比较所得到的数据,又称为度量数据 - **连续性随机变量**:变量可以在某个区间内取任一实数,即变量的取值可以是连续的  ## 数据的频率分布 - **频率分布**反映一组数据中不同观测值出现的频率 - 用图和表对样本数据进行定性归纳 ### 频数(率)图 此图为条形图(柱形图) 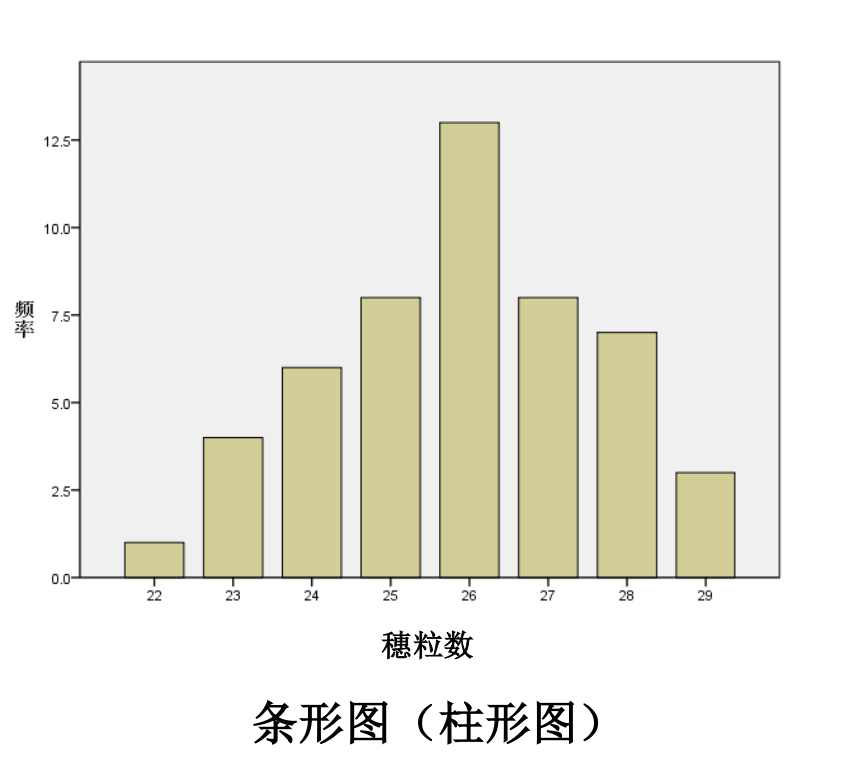 ## 连续型数据频数表和频数图的绘制 ### 1. 求全距(极差) 全距是资料(样本)中最大值与最小值之差,又称为极差(range),用$R$表示,即: $$ R = max - min $$ ### 2. 确定组数 组数对多少视样本含量及资料的变动范围大小而定,一般以反映**资料的规律性**为原则 | 样本含量(n) | 组数 | | ------- | ----- | | 30-60 | 5-8 | | 60-100 | 7-10 | | 100-200 | 9-12 | | 200-500 | 10-18 | | 500以上 | 15-30 | ### 3. 确定组距 每组最大值与最小值之差称为组距,记为 $i$,分组时要求各组的组距相等,即: $$ 组距(i) = \frac{全距(R)}{组数} $$ ### 4. 确定组限及组中值 各组的最大值与最小值称为**组限**。最小值称为**下限**,最大值称为**上限** 每一组的中点值称为**组中值**,是该组的代表值 组中值与组限电关系如下:(平均数) $$ 组中值 = (组下限+组上限) / 2 $$ 第一组组中值确定以后,第一组组中值加上组距就是下一组的组中值;以此类推,可以求出各组的组中值 ### 5. 确定组界(Class Boundaries) 由于数据通常是连续的(可能是小数),而测量值是四舍五入的,因此组界要调整,以反映实际的数值范围: - **下组界(Lower Class Boundary, LCB)** = 组下限 - 0.5 - **上组界(Upper Class Boundary, UCB)** = 组上限 + 0.5 例如,对于组限 37~39: - 下组界 = 37 - 0.5 = 36.5 - 上组界 = 39 + 0.5 = 39.5 | 组限(整数表示) | 组界(真实范围) | | -------- | --------- | | 37~39 | 36.5~39.5 | | 40~42 | 39.5~42.5 | | 43~45 | 42.5~45.5 | ### 绘制连续性数据频数直方图 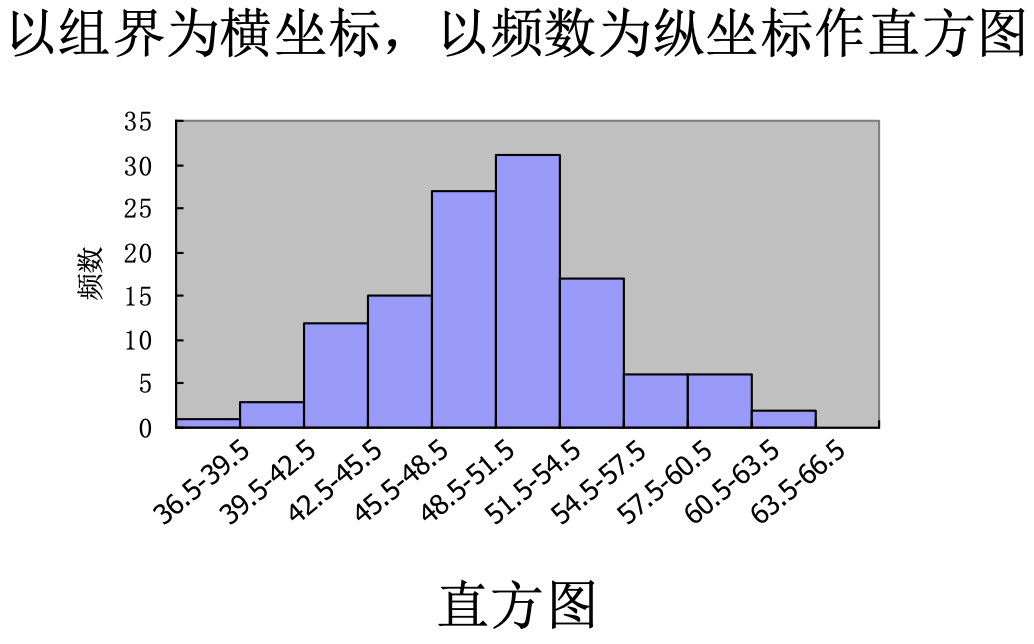 ### 使用 R 绘制连续性数据频数直方图 1. 基本绘制频数直方图 ```r # 生成示例数据(假设是体重数据) data <- c(37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49) # 绘制频数直方图 hist(data, main = "频数直方图", # 标题 xlab = "体重 (kg)", # X 轴标签 ylab = "频数", # Y 轴标签 col = "lightblue", # 颜色 border = "black") # 直方图边框颜色 ``` 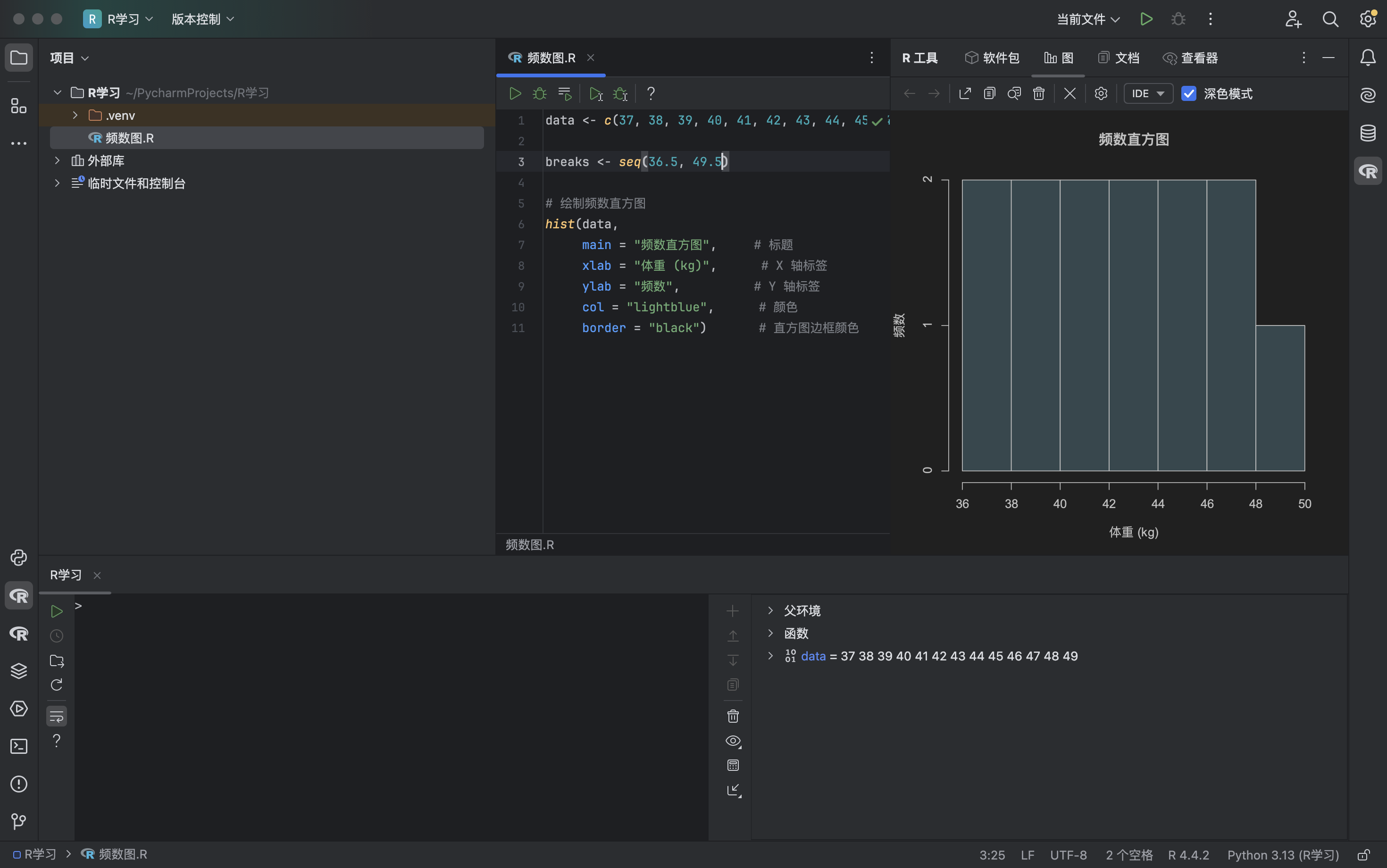 2. 按组界划分的频数直方图 ```r data <- c(37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49) # 指定分组区间 breaks <- seq(36.5, 51.5, by = 2) # 从 36.5 到 49.5,间隔 3 # 绘制直方图 hist(data, breaks = breaks, main = "按组界划分的频数直方图", xlab = "体重 (kg)", ylab = "频数", col = "skyblue", border = "black") ``` 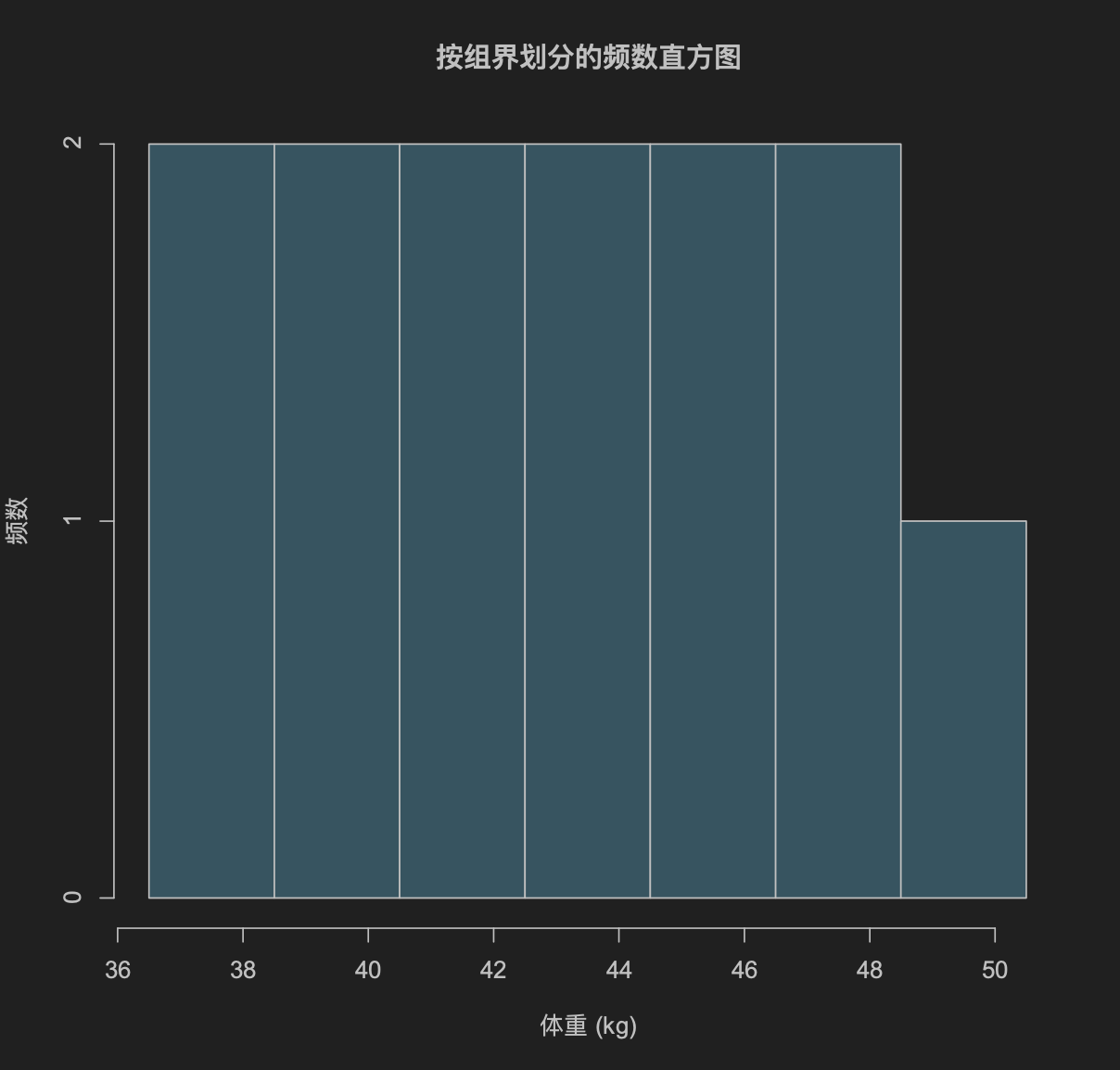 图中的下组限为36,上组限为50 **为什么上组限不使用49.5?** 其中的组距为2,要保证组距一样 ## 常见误区 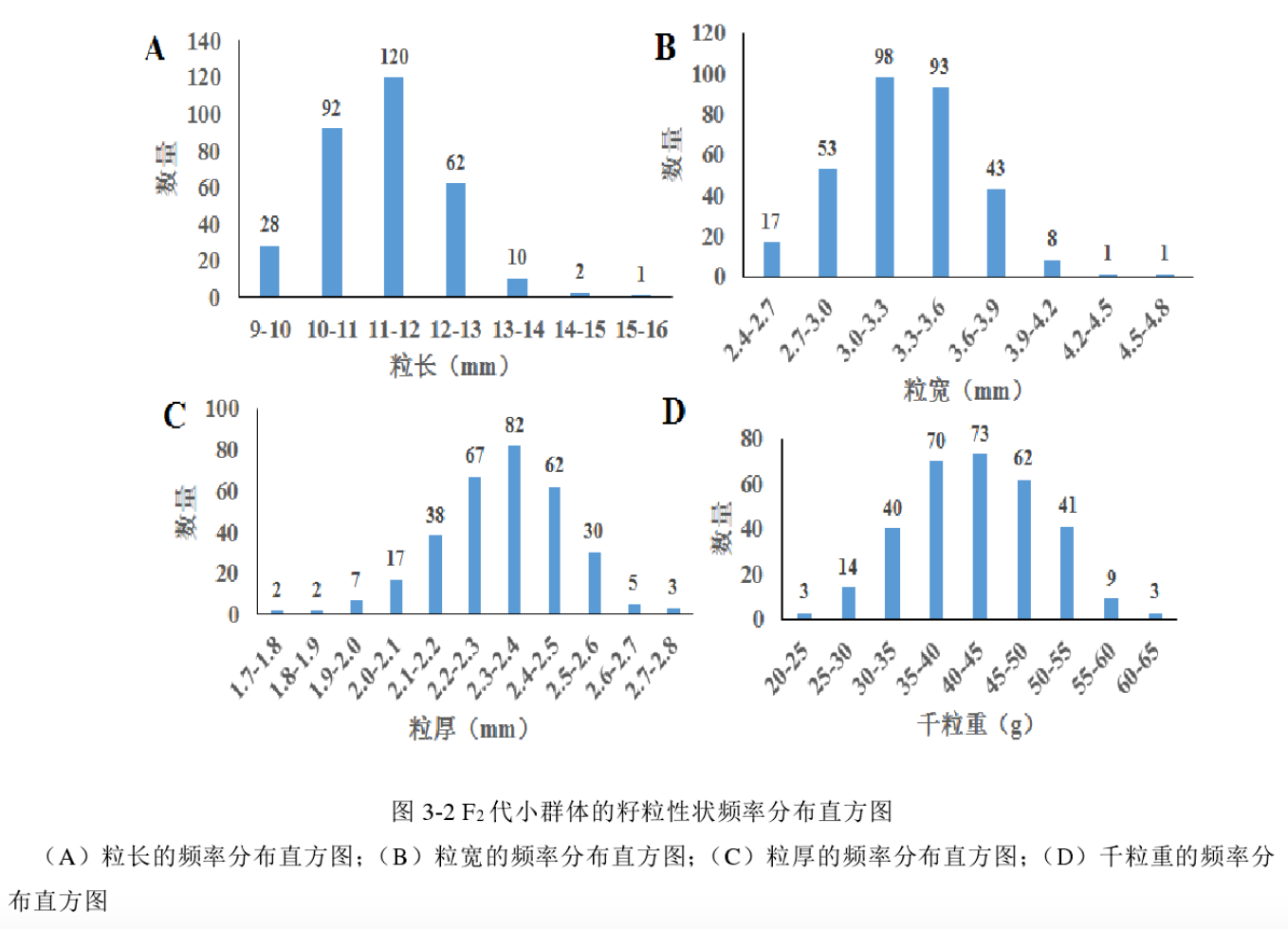 直方图中,相邻的组之间要连在一起,因为直方图中的面积是具有实际意义的,表示连续数据  条形图(柱形图)就没有这样的规定 ### 条形图(柱形图)与直方图之间的区别与关系 条形图(**Bar Chart**)和直方图(**Histogram**)虽然看起来相似,但它们有 **本质区别**: | **对比项** | **条形图(Bar Chart)** | **直方图(Histogram)** | |------------|-------------------------|-------------------------| | **数据类型** | 适用于 **离散数据**(如分类数据) | 适用于 **连续数据**(如身高、体重) | | **X 轴** | **类别(分类变量)** | **数值区间(连续变量)** | | **Y 轴** | **频数或相对频率** | **频率密度(区间内的频数)** | | **柱子间隔** | **有间隔**,每个柱子表示一个独立的类别 | **无间隔**,柱子连续,表示数值区间 | | **示例数据** | 城市、性别、职业、品牌等 | 体重、身高、温度、年龄等 | --- #### **1. 条形图(Bar Chart)** 适用于**离散数据**,如不同品牌的销量、不同国家的人口等。 ##### **示例(不同颜色的苹果销售量)** ```r fruit_counts <- c(红苹果 = 50, 绿苹果 = 30, 黄苹果 = 20) barplot(fruit_counts, main = "不同颜色苹果销售量", col = "skyblue") ``` **特点**: - `x` 轴表示 **类别**(苹果颜色)。 - `y` 轴表示 **数量**(销量)。 - **柱子之间有间隔**,因为不同类别之间没有连续性。 --- #### **2. 直方图(Histogram)** 适用于**连续数据**,如人的身高、体重、分数分布等。 ##### **示例(学生身高分布)** ```r heights <- c(150, 160, 165, 170, 172, 175, 180, 185, 190, 195) hist(heights, breaks = seq(150, 200, by = 10), col = "lightblue", main = "身高分布直方图") ``` **特点**: - `x` 轴表示 **连续变量的区间**(身高范围)。 - `y` 轴表示 **频数(区间内的人数)**。 - **柱子之间没有间隔**,表示数据的连续性。 --- #### **直方图 vs. 条形图的示意图** ##### **条形图(有间隔)** ``` 类别1 ███ 类别2 ██████ 类别3 ████ ``` ##### **直方图(无间隔)** ``` (0-10] ███ (10-20] ██████ (20-30] ████ ``` --- #### **总结** - **条形图** 适用于 **分类数据**(城市、职业、品牌)。 - **直方图** 适用于 **连续数据**(身高、体重、温度)。 - **条形图有间隔**,**直方图无间隔**。 - **直方图的 X 轴是区间**,**条形图的 X 轴是类别**。 如果你要绘制**体重分布**,用 **直方图**;如果你要绘制**不同颜色苹果的销售量**,用 **条形图**。 ## 样本特征数 定义:描述样本频率分布特征的数 根据表示的意义不同可分为两种: - 表示**集中趋势**或中心位置 - 表示**离中**趋势或变异 ### 表示集中趋势或中心位置 #### 算术平均数(arithmetic mean) 简称为**平均数(mean)** $$ \bar{x} = {{x_{1}+x_{2}+···+x_{n}}\over{n}} = {{\sum^n_{i=1}x_{i}}\over{n}} $$ 或 $$ \bar{x} = {\sum{x}\over{n}} $$ #### 求和符号的运算法则: - 常数可以提刀总和符号之外 $$ \sum^n_{i=1}{ax_{i}} = a \sum^n_{i=1}{x_{i}} $$ - 常数的总和等于该常数的$n$倍 $$ \sum^n_{i=1}{a} = na $$ - 代数和的总和等于总和的代数和 $$ \sum^n_{i=1}(x_{i}+y_{i}-z_{i}) = \sum^{n}_{i=1}{x_{i}} + \sum^n_{i=1}y_{i} - \sum^n_{i=1}z_{i} $$ #### 平均数的计算方法 - 对非频数资料的计算 - 直接法(离散型数据) $$ \bar{x} = {{x_{1}+x_{2}+···+x_{n}}\over{n}} = {\sum^n_{i=1}{x_{i}}\over{n}} $$ - 对频数资料的计算 - 加权法(连续型数据) $$ \bar{x} = {{\sum^k_{i=1}f_{i}x_{i}}\over{\sum^k_{i=1}f_{i}}} = {\sum{fx}\over{\sum f}} $$ 其中,$x$为组值(组中值);$f$为频数 对于**离散型数据**来说,使用直接法和加权法算出来的平均数是一样的  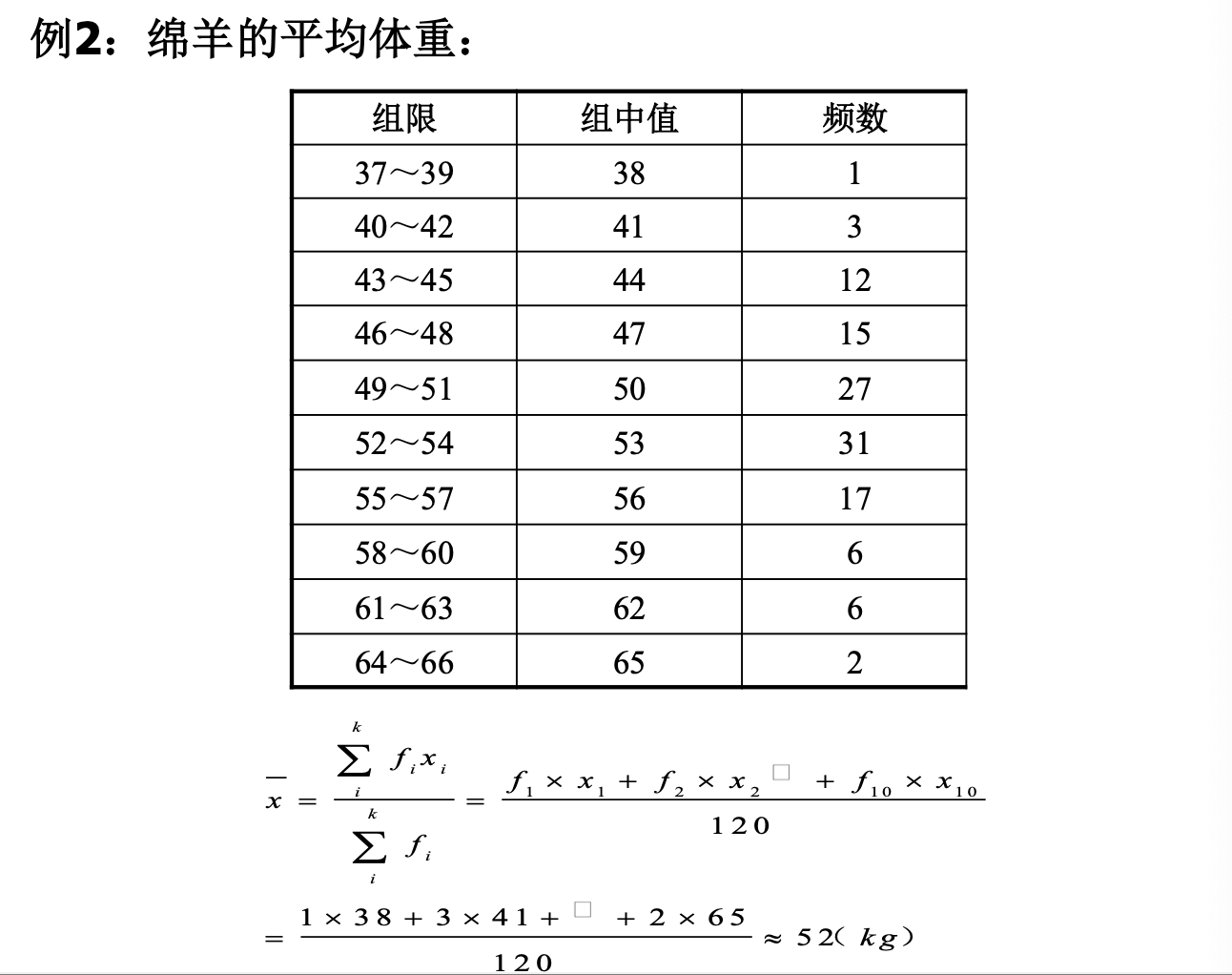 #### 中位数与众数 **中位数**:位于有序数列中点上的数,以$M_{d}$表示 **众数**:具有最高频数的组值或中值,以$M_{o}$表示 ### 表示离中趋势或变异 #### 范围(range) 范围又称全距,记为$R$,是一组数据中的最大值与最小值的差,$R=max-min$ #### 平均离差(mean deviation) **平均离差**:求离均差**绝对值**的和,然后用$n$去除 $$ MD = {\sum{\lvert{x - \bar{x}}\rvert}\over n} $$  #### 方差(variance) 所有离均差的平方和相加称为离差平方和,用$ss$表示 样本的方差公式: $$ s^2 = {{\sum^n_{i=1}{(x_{i}-\bar{x})}\over{n-1}}} $$ 整体的方差公式: $$ \sigma^2 = {\sum^n_{i=1}(x_{i}-\bar{x})\over{n}} $$ 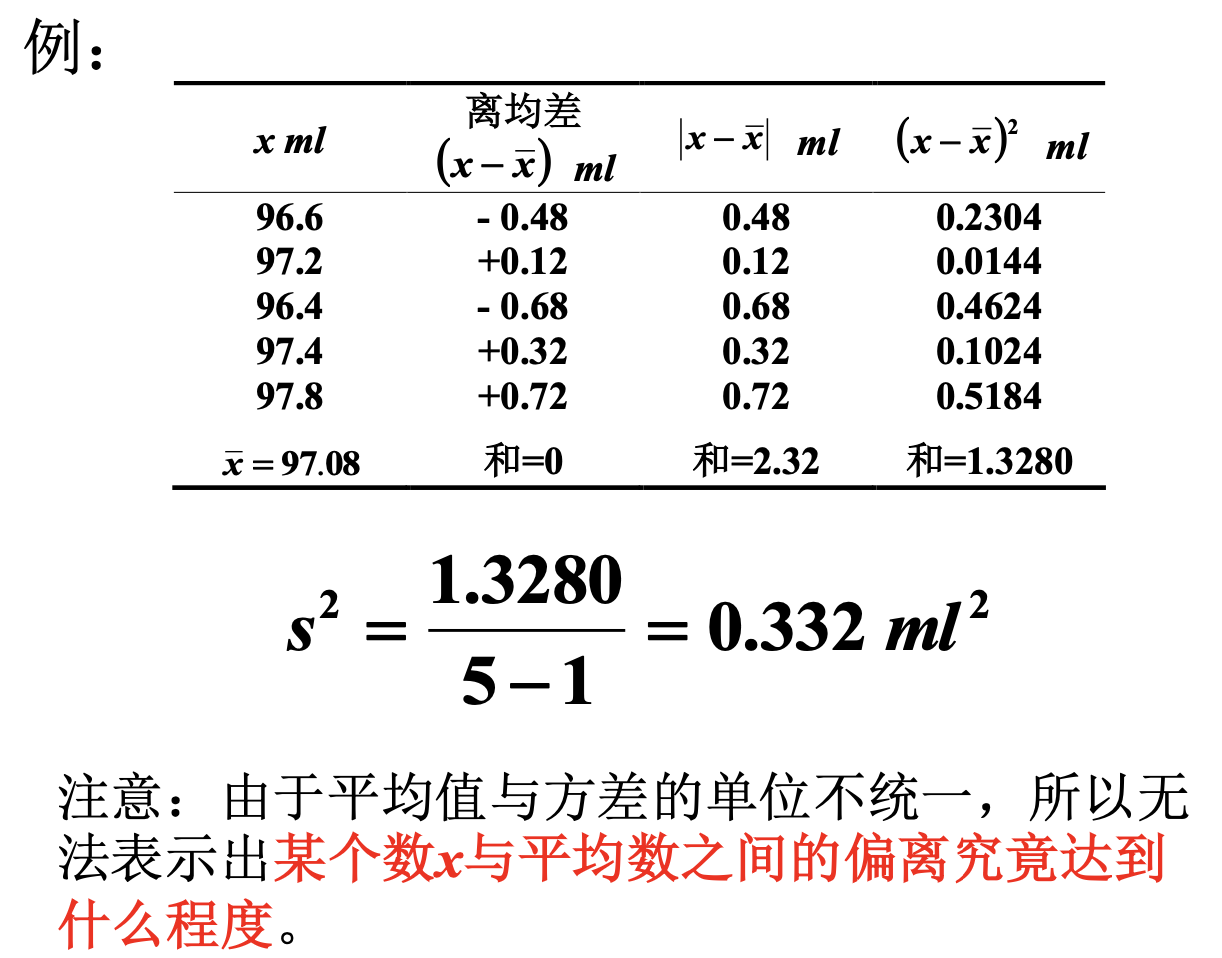 #### 标准差(standard deviation) 开方后的方差称为标准差,记为$s$ $$ s = \sqrt{ {\sum^n_{i=1}{(x_{i}-\bar{x})^2}}\over{n-1} } $$ 同时对于**非频数资料的标准差**存在另外一种计算方法: $$ s = {\sqrt{ {\sum^n_{i=1}{x^{2}_{i}}-{{\left( \sum^n_{i=1}x_{i} \right)^2}\over{n}}\over{n-1}} }} $$ 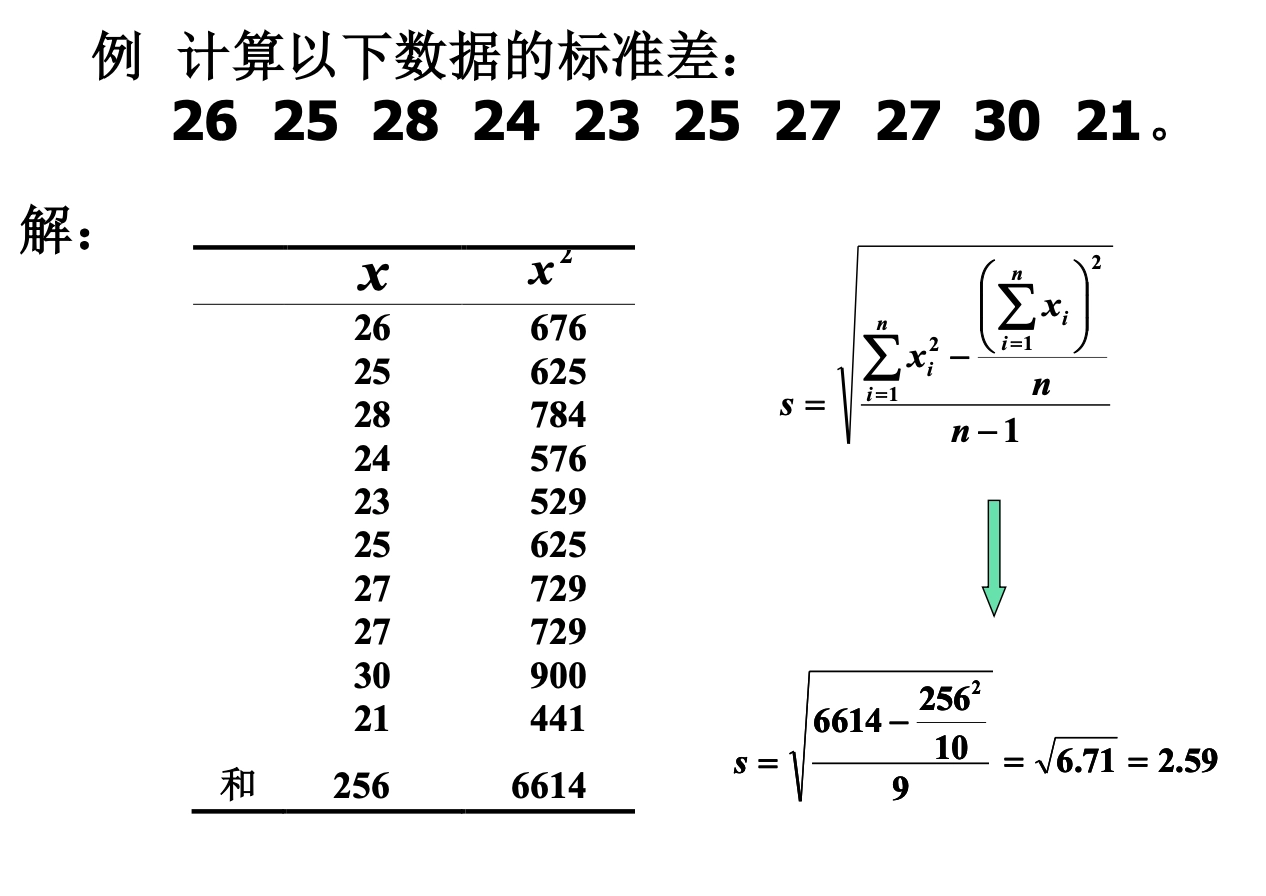 对于**频数资料的标准差**也存在另外一种计算方法: $$ s = {\sqrt{ {\sum^k_{i=1}{(fx^2)_{i} - {{\left[ \sum^k_{i=1}{fx}_{i} \right]^2}\over{N}}\over{N-1}}} }} $$ 其中,$f$ = 频数,$x$ = 组值(组中值),$N$ = 总频数,$k$ = 组数 标准差离散程度的实际意义: 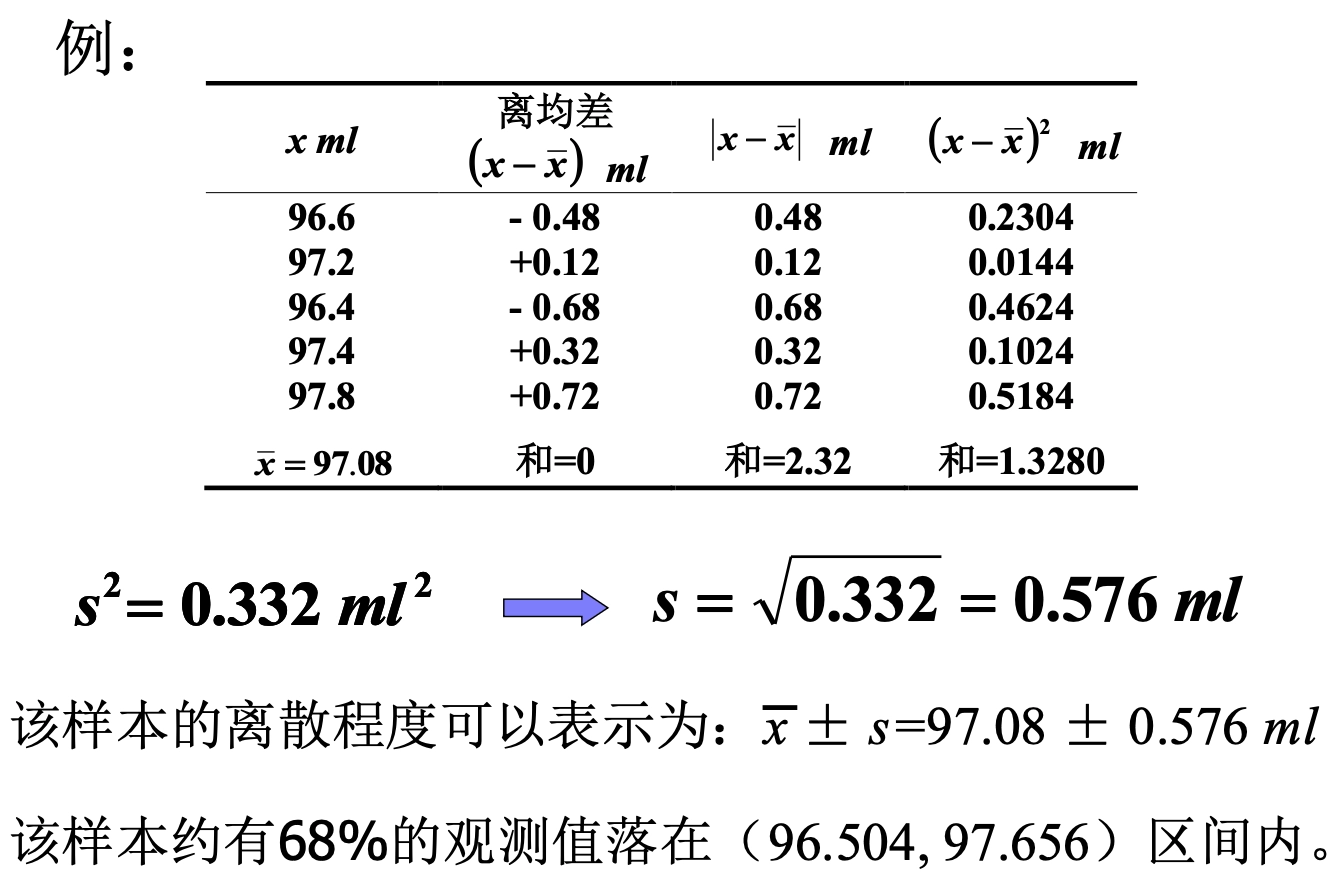 #### 小结 抽样理论证明:用标准差估计总体离散程度最可靠,平均离差次之 ### 样本的其他特征数 #### 偏斜度(skewness) - 度量数据围绕众数呈不对称的程度 - 大小说明曲线倾斜的程度 $$ g_{1} = {{m_{3}\over{m^{3/2}_{2}}}} = {{\sum^n_{i=1}(x_{i}-\bar{x})^3}\over{\left( \sum^n_{i=1}(x_{i}- {\bar{x}}^2)\right)}^{3\over_{2}}} $$ 从图像上来看: - 众数 < 平均数(左偏) - 众数 > 平均数(右偏) 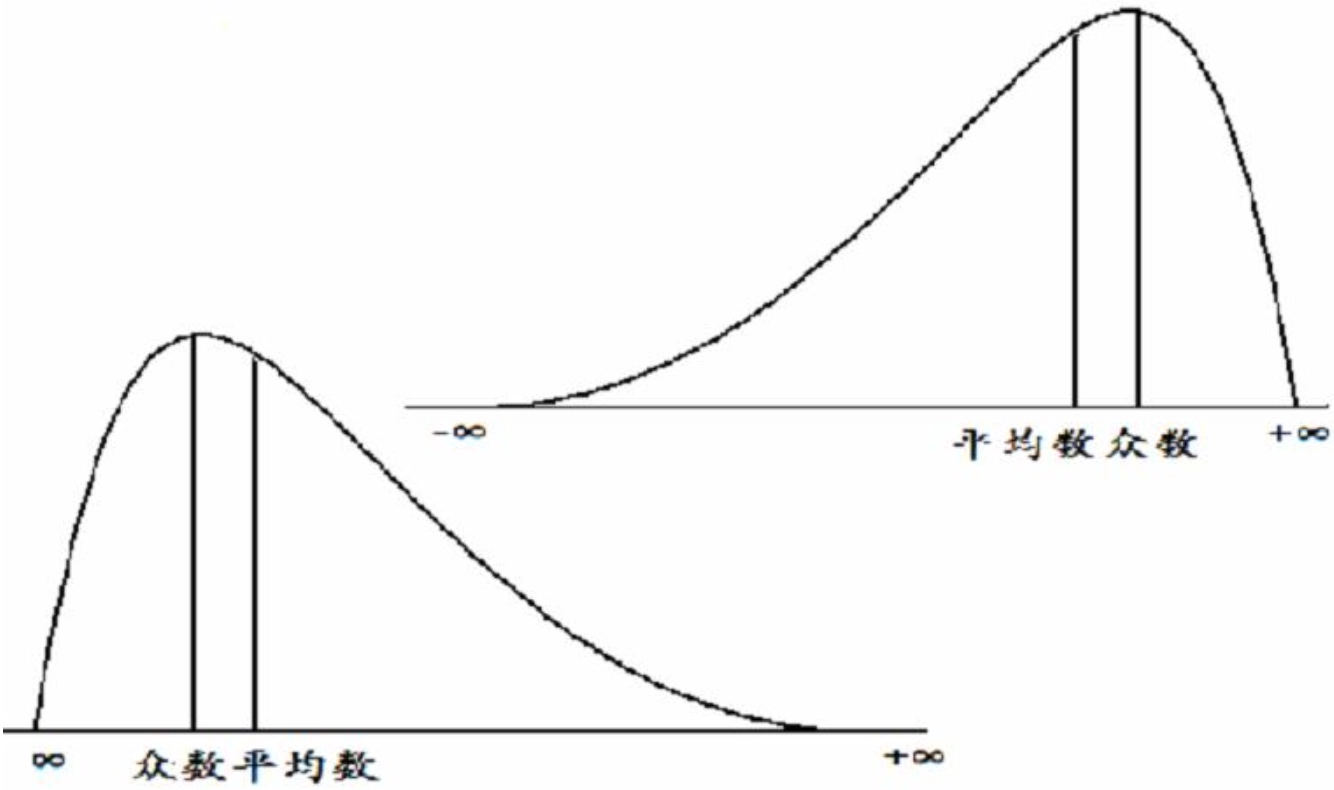 #### 陡度(kurtosis) - 用来量度曲线形状 - $g_{2}=0$,则认为数据是正态的;$g_{2}>0$,曲线过于陡峭;$g_{2}<0$,曲线过于平坦 $$ g_{2} = {{m_{4}\over{m^2_{2}}}-3}={{\sum^n_{i=1}(x_{i}-\bar{x})^4}\over{(\sum^n_{i=1}(x_{i}-\bar{x})^2)^2}}-3 $$ 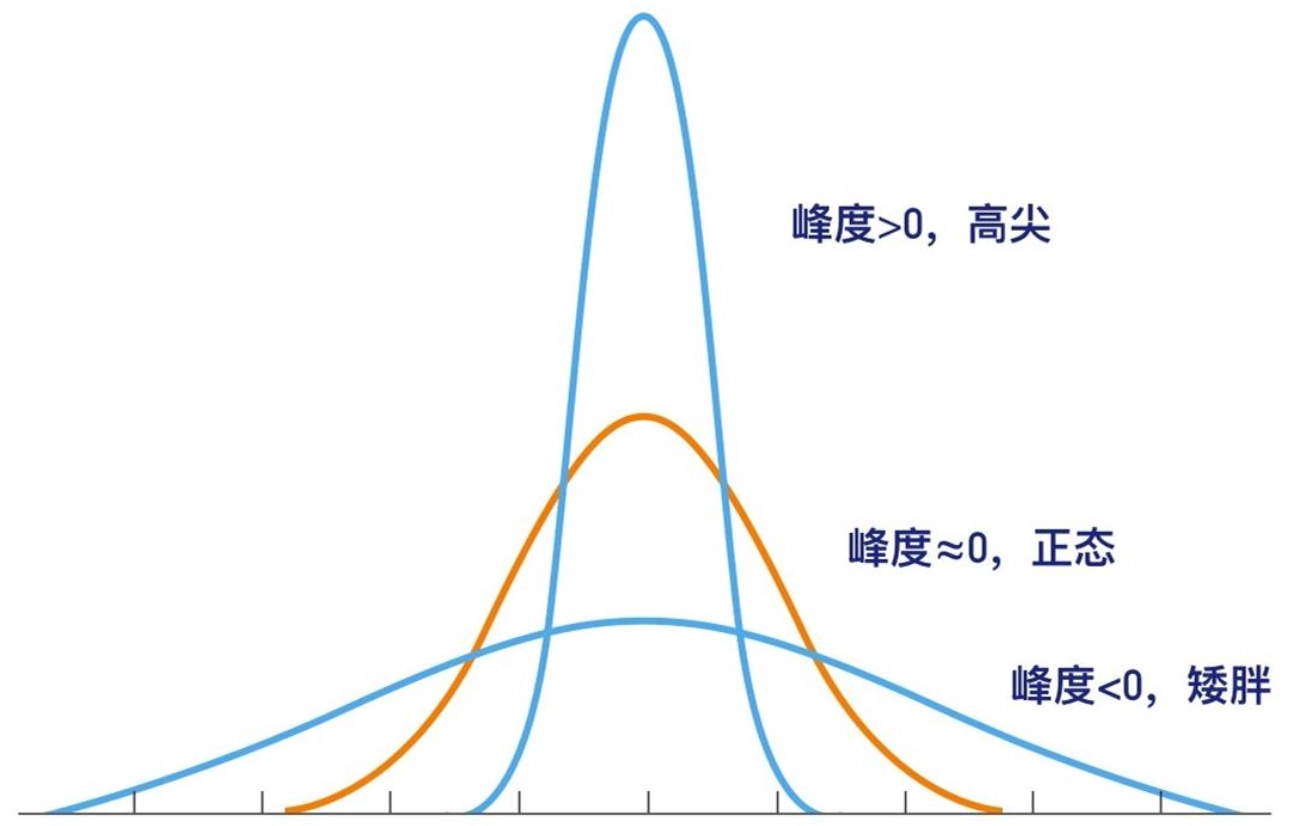 当进行两个或多个资料变异程度的比较时,如果**度量单位**与**平均数**都相同,可以直接利用标准差来比较 #### 变异系数(coefficient of variability, CV) 如果单位或者平均数不同时,比较其变异程度就不能采用标准差,而需采用标准差与平均数的比值(相对值)来比较,称为**变异系数** $$ CV = {{s}\over{\bar{x}}} $$  最后修改:2025 年 03 月 11 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏
此处评论已关闭