Loading... ## 概率 ### 概率的定义 **概率**:事件在试验结果中出现可能性大小的定量计量 ### 概率与频率的区别 - 概率:抽象的,理论的,某情况**应该**发生几次 - 频率:具体的,实际的,某情况**实际**发生了几次 ### 概率的性质 1. 必然事件($W$)的概率为1,即$P(W)=1$ 2. 不可能事件($V$)的概率为0,即$P(V)=0$ 3. 任何事件($A$)的概率均满足 $0\le P(A) \le 1$ ### 古典概型 需要满足以下两个条件: - 随机试验的全部可能的结果(基本事件数)是有限的 - 各基本事件间是互不相容且等可能的 $$ P(A) = m / n $$ 求古典概型的基本步骤: - 算出所有基本事件的个数$n$ - 求出事件$A$包含的所有基本事件数$m$ - 代入公式$P(A)=m / n$,求出$P(A)$ ### 概率的运算法则 #### 概率的加法法则 $$ P(A\cup B) = P(A)+P(B)-P(A\cap B) $$ 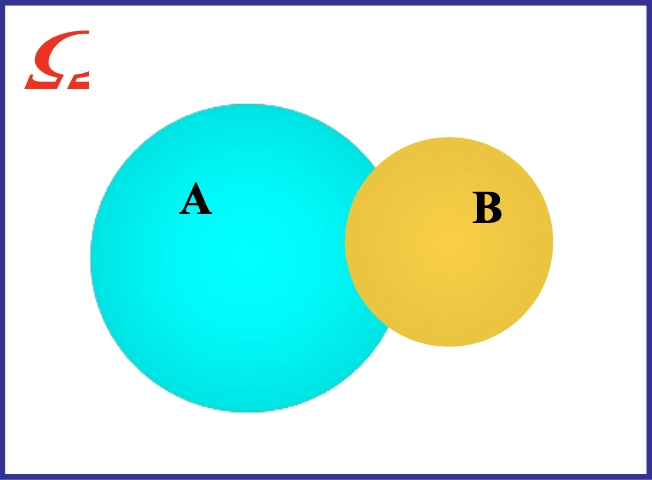 如果A、B之间不存在交集,则: $$ P(A\cup B) = P(A) + P(B) $$ 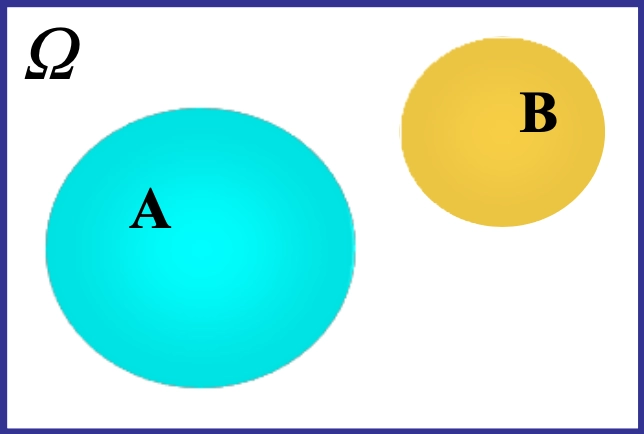 可以对其进行推广,如果有限个事件两个互不相容,则: $$ P(A_{1}\cup A_{2}\cup\dots\cup A_{n}) = P(A_{1})+P(A_{2})+\dots+P(A_{n}) $$ 事件$A$的概率和它的对立事件$\bar{A}$的概率的关系: $$ P(\bar{A})=1-P(A) $$  ### 条件概率 **定义**:设$A、B$为随机试验$E$的两个事件,且$P(B)>0$,则称$P(A|B)$为在事件$B$已发生的情况下,事件$A$发生的条件概率 $$ P(A|B) = {P(AB)\over{P(B)}} $$ 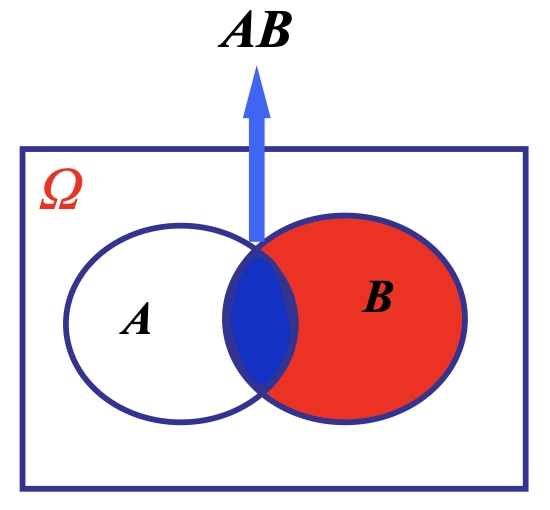 - $P(A|B)$以$B$发生为条件,样本空间缩小为$B$ - $P(A|B)$相当于把$B$看作新的样本空间,求$AB$发生的概率  ## 贝叶斯公式 设$A_{1},A_{2},\dots,A_{n}$是两两互斥的事件,且$P(A_{i})>0,i=1,2,\dots,n$;另有一事件$B$,它总是与$A_{1},A_{2},\dots,A_{n}$之一同时发生,则: $$ P(A_{i}|B) = \frac{{P(A_{i})P(B|A_{i})}}{\sum^n_{j=1}P(A_{j})P(B|A_{j})} $$    ### 小结 贝叶斯公式的本质是根据随机事件$B$的发生提供的信息,对事件$A_{i}$发生的概率进行重新的估计 ## 概率分布 **随机变量**:(random variable) - ~~随机试验中被测定的量~~ 研究对象,被测定的指标,常以大写的拉丁字母表示,如$X、Y$ - 用随机变量的关系表示事件,如$X\le{3}$ **观测值**:(observation) - 随机变量所取得的值,常以带下标的小写字母表示,如$x_{i}、y_{i}$ **离散型随机变量**:(discrete random variable) - 随机变量可能取得的数值为有限个 **连续性随机变量**:(continuous random variable) - 随机变量可取某一(有限或无限)区间内的任何数值 ### 离散型概率分布 **概率函数**:(probability function) - 将随机变量$X$所取得值$x$的概率$P(X=x)$写成$x$的函数$p(X)$,这样的函数称为随机变量$X$的概率函数 - $p(x)=P(X=x)$ 概率函数应该满足: $$ p(x)\ge{0}, \sum_{x}p(x)=1 $$ **概率分布**:(probability distribution) - 将$X$的一切可能值$x_{1},x_{2},\dots,x_{n},\dots$以及取得这些值的概率$p(x_{1}),p(x_{2})\dots,p(x_{n},\dots)$排列起来,即构成离散型随机变量的概率分布 - 可用概率分布表和概率分布图表示 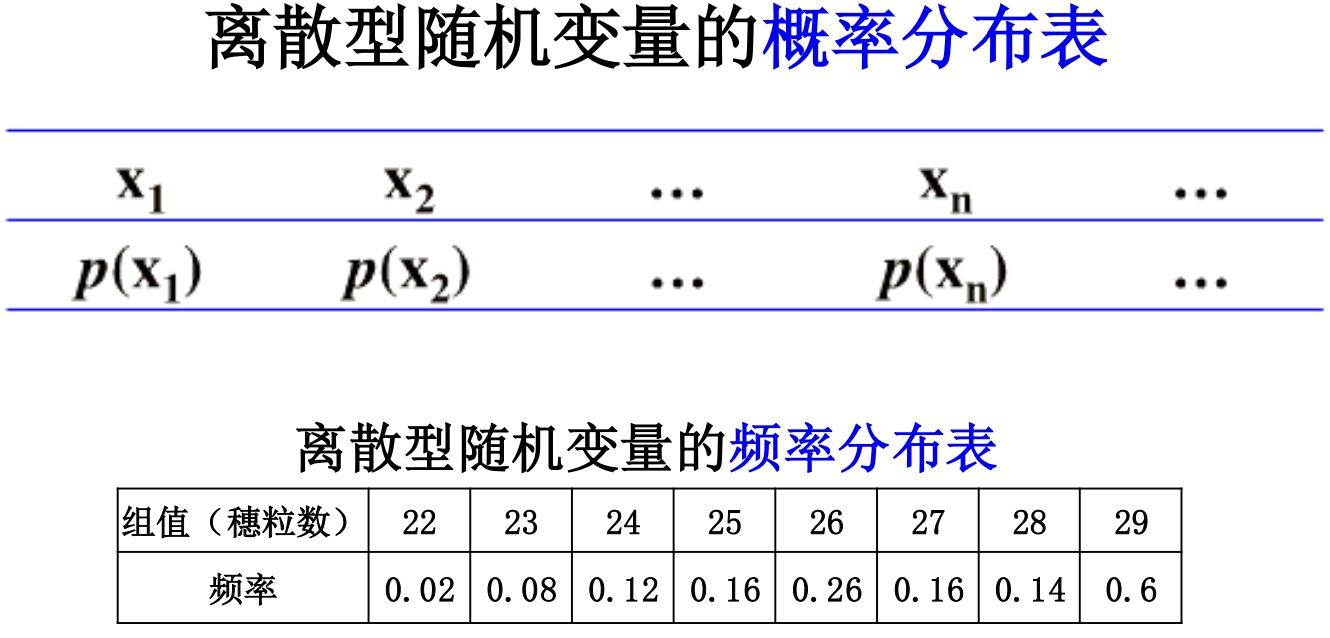 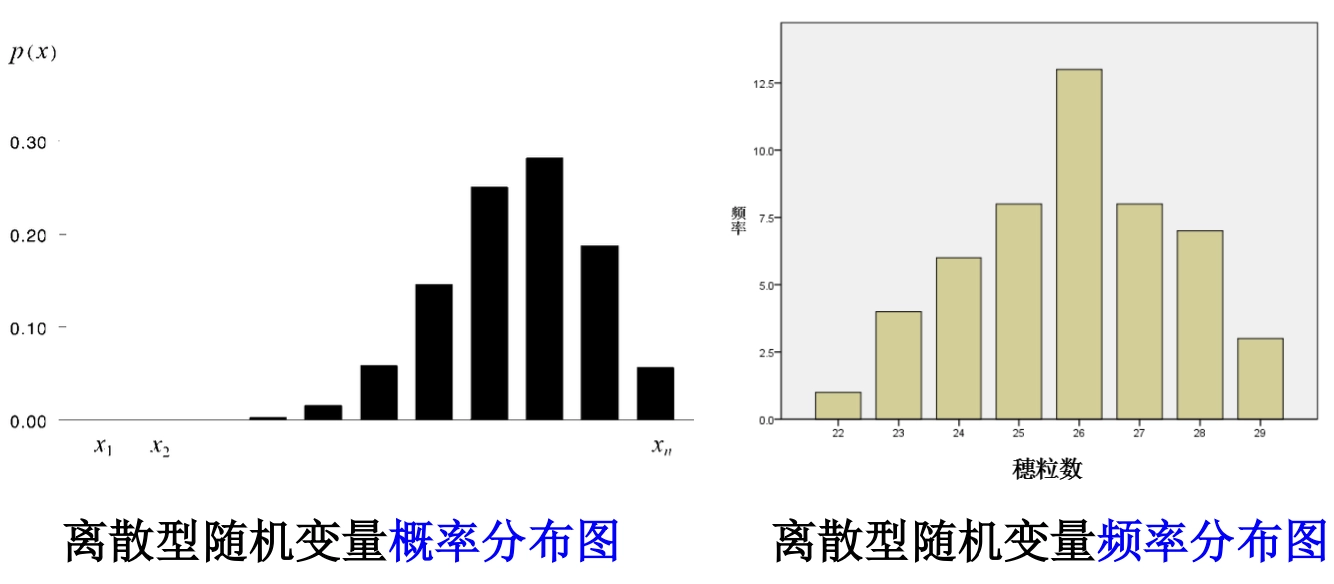 **分布函数**:(distribution function) - 随机变量**小于等于某一可能值**($x_{0}$)的概率,记为$F(x_{0})$: $$ F(x_{0}) = \sum_{x_{i}\le{x_{0}}}p(x_{i})=P(X\le{x_{0}}) $$ **密度函数**:(density function) - 随机变量$X$的值落在区间$(x, x+\Delta{x})$内的概率为$P(x<X<x+\Delta{x})$,当$\Delta{x}\to{0}$时,$[P(x<X<x+\Delta x)]/\Delta{x}$的极限表示随机变量$X$在点$x$处的概率密度,用符号$f(x)$表示,称$f(x)$为随机变量$X$的密度函数 $$ f(x)=\lim_{ \Delta{x} \to 0 }{{P(x<X<x+\Delta{x})}\over{\Delta{X}}} $$ **分布曲线**:(distribution function) 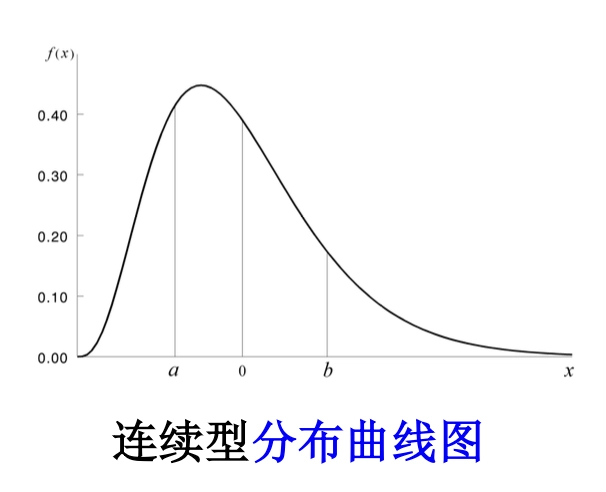 概率$P(a<X<b)$等于区间$a,b$所夹的曲线下面积: $$ P(a<X\le{b})= \int_{a}^b f(x)dx $$ **分布函数**:(distribution function) 随机变量取得小于$x_{0}$的值的概率,记为$F(x_{0})$,则有: $$ F(x_{0})=P(X\le{x_{0}})=\int_{-\infty}^{x_{0}}f(x)dx, F(-\infty)=0, F(\infty)=1 $$ 对于任意两点$a$和$b$,存在$P(a<X\le{b})=F(b)-F(a)$成立 ## 总体特征数(population characteristic) ### 定义 描述频率分布特征的数字称为总体特征数,随机变量的**数学期望**(总体平均数)和**方差**是两个主要的特征数 ### 数学期望 #### **离散型** 观测值: $$ \bar{x}={{\sum_{i=1}^{k}f_{i}x_{i}}\over{n}}=\sum_{i=1}^{k}({f_{i}\over{n}})x_{i} $$ 总体: $$ \mu=E(X)=\sum_{x}p(x)x $$ #### 连续型 $$ \mu=E(X)=\int_{-\infty}^{\infty}xf(x)dx $$ 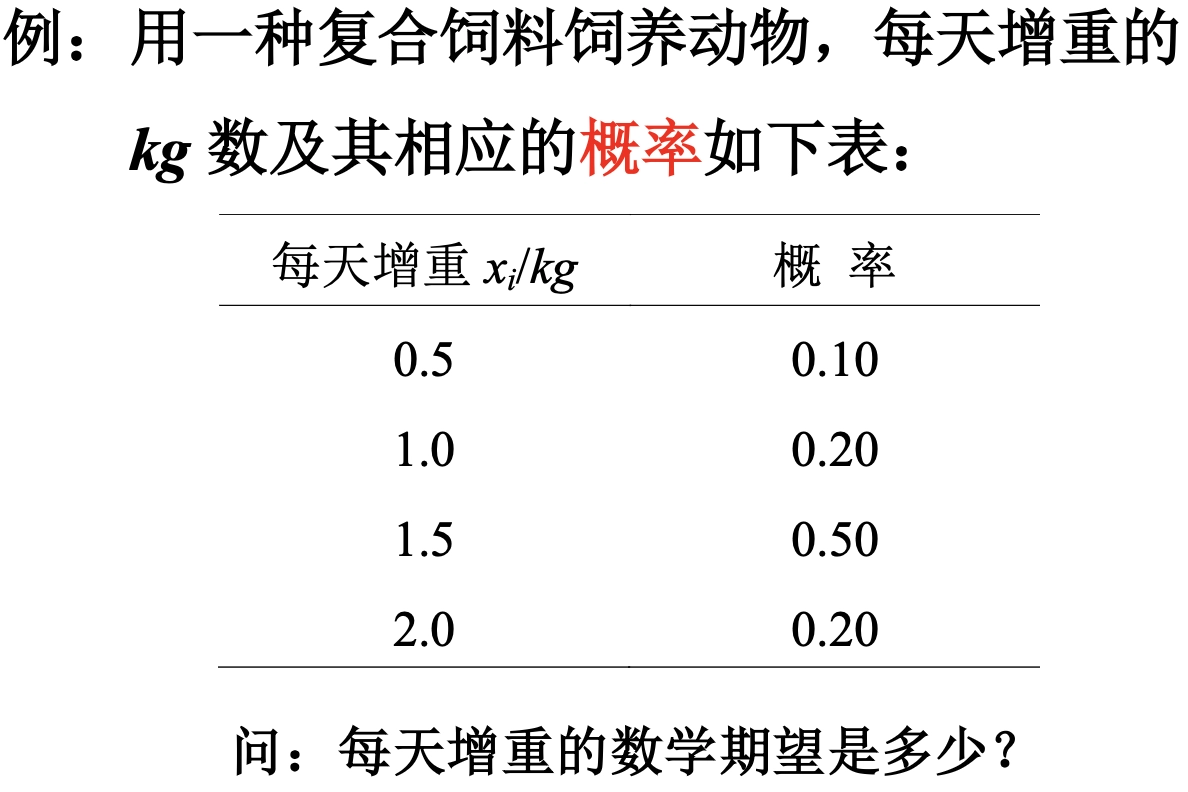  ### 方差 #### 离散型 观测值: $$ s^2=\sum_{i=1}^{k}({f_{i}\over{n-1}})(x_{i}-\bar{x})^2 $$ 总体: $$ \sigma^2=\sum_{x}p(x)(x-\mu)^2=E[(x-\mu)^2] $$ 便捷式算法: $$ \sigma^2=E(X^2)-(E(X))^2=\sum_{i=1}^np(x_{i})x_{i}^2-\left( \sum_{i=1}^np(x_{i})x_{i} \right)^2 $$ #### 连续性 $$ \sigma^2=E[(X-\mu)^2]=\int_{-\infty}^{\infty}(x-\mu)^2f(x)dx $$ 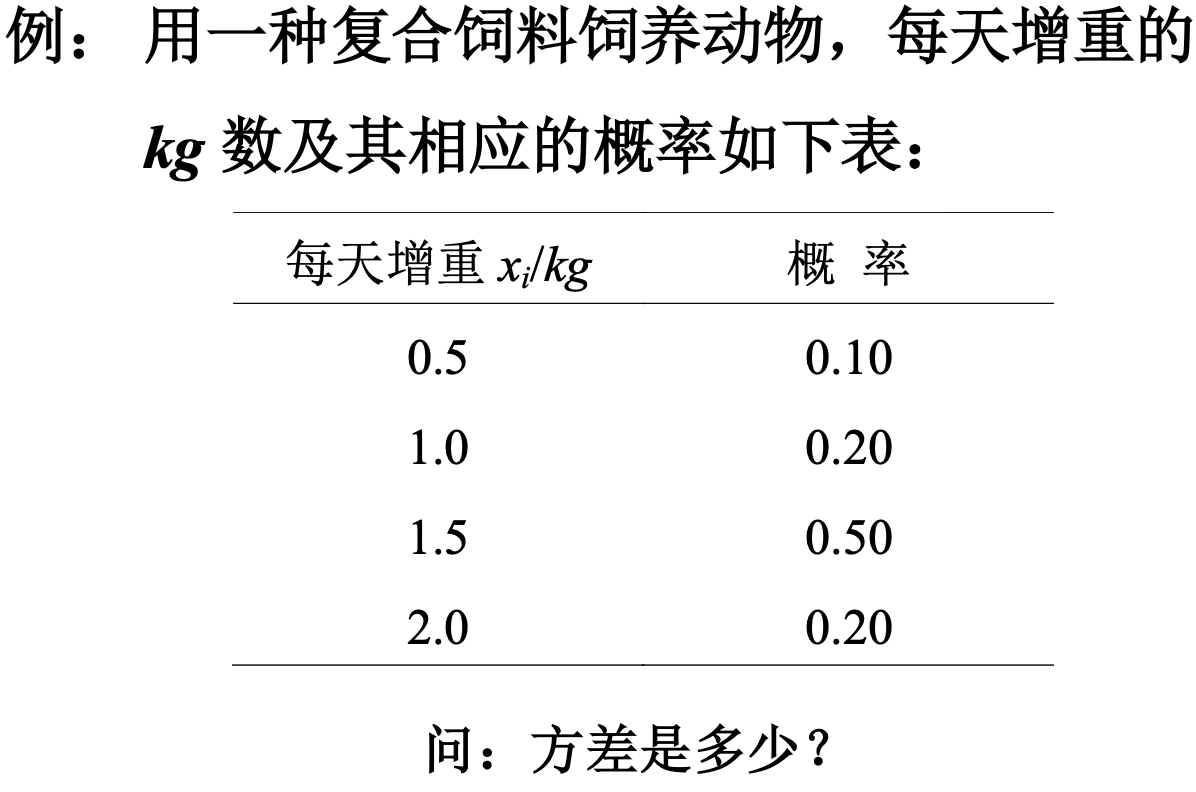 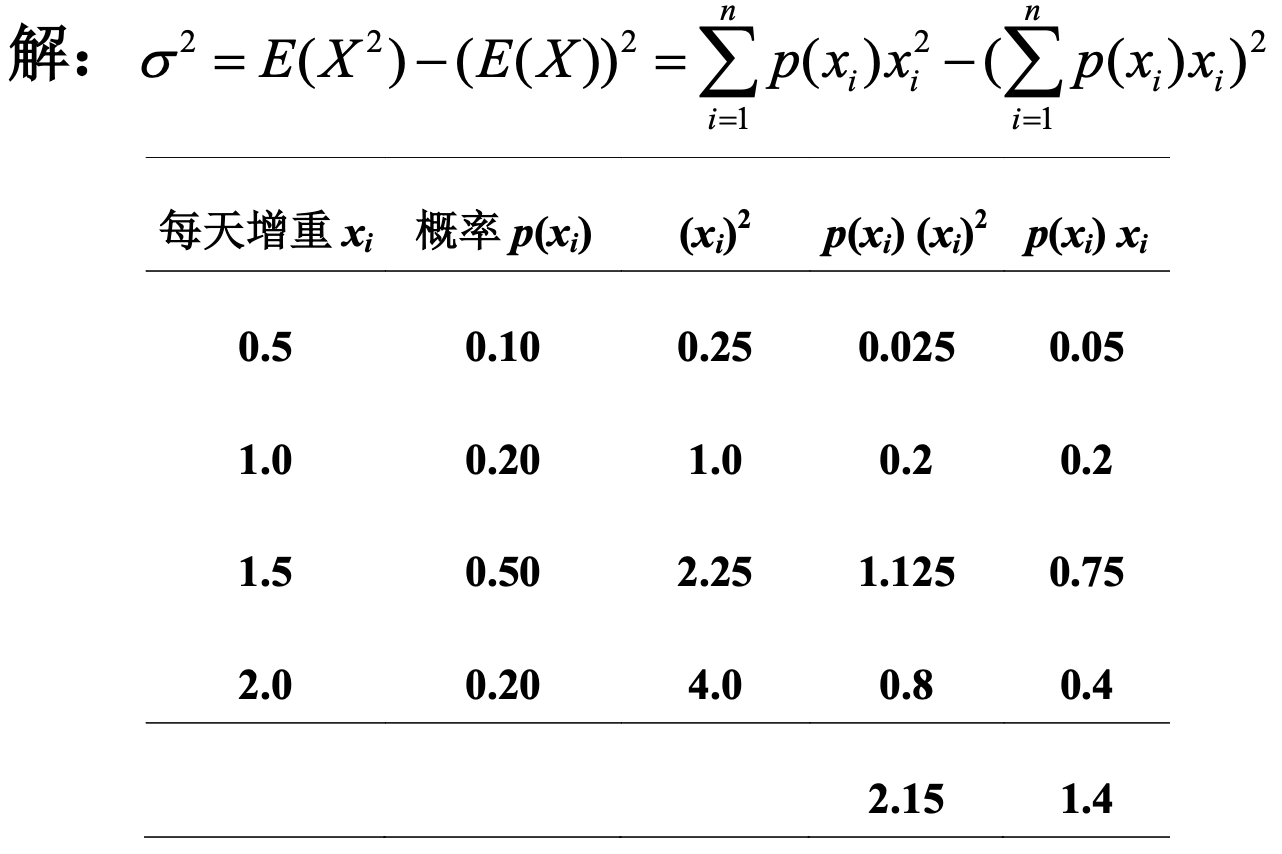 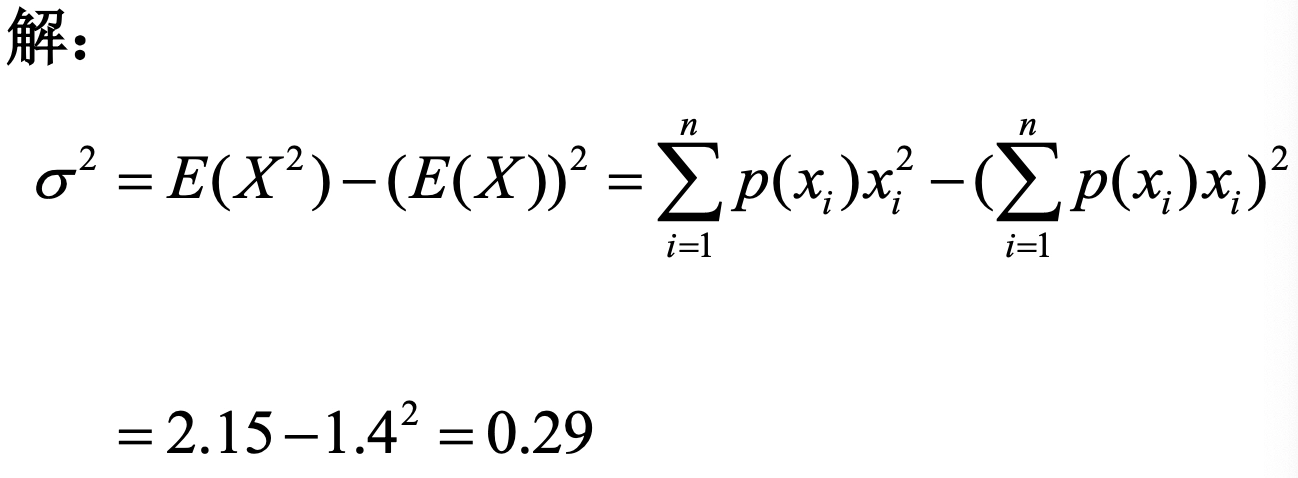 ### 数学期望与方差的运算 #### 数学期望的运算法则 其中$c$为常数: $E(c)=c$ $E(cX)=cE(X)$ $E(X+c)=E(X)+c$ $E(cX+A)=cE(X)+A$ #### 总体方差的运算法则 **总体方差**记为$var(X)$,其中$c$为常数: $var(X)=E[(X=\mu)^2]$ $var(cX)=c^2var(X)$ $var(X+c)=var(X)$ $var(cX+A)=c^2var(X)$ 最后修改:2025 年 03 月 17 日 © 允许规范转载 赞 如果觉得我的文章对你有用,请随意赞赏
此处评论已关闭